Question

The angle of intersection between the curve ${{x}^{2}}=8y$ and ${{y}^{2}}=8x$ at $\left( 0,0 \right)$ is:
(A) $\dfrac{\pi }{4}$
(B) $\dfrac{\pi }{3}$
(C) $\dfrac{\pi }{6}$
(D) $\dfrac{\pi }{2}$

Answer 1

Hint: First of all, differentiate the equations ${{x}^{2}}=8y$ and ${{y}^{2}}=8x$ with respect to x and the values of $\dfrac{dy}{dx}$ after differentiating both of the equations. Now, put $\left( 0,0 \right)$ in the values of $\dfrac{dy}{dx}$ . We know that, $\tan 0=0$ and $\tan \dfrac{\pi }{2}=\infty$ . Now, solve it further and get the angle between the tangents.

Complete step-by-step answer:
According to the question, it is given that we have the equation of two curves,
${{x}^{2}}=8y$ …………………(1)
${{y}^{2}}=8x$ …………………..(2)
We have to find the angle of intersection between these two curves at the point whose coordinate is $\left( 0,0 \right)$ .
For the angle of intersection between these two curves, we have to find the slope of the tangent at the point of intersection of these two curves.

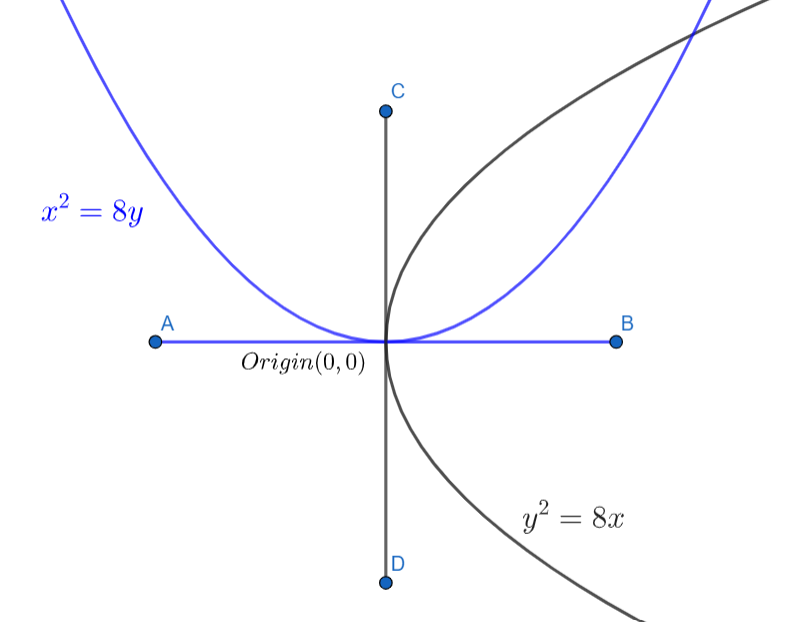
Let us find the slope of the tangent AB of the curve ${{x}^{2}}=8y$ at the point $\left( 0,0 \right)$ .
Differentiating with respect to x, the LHS and RHS of the equation of the curve ${{x}^{2}}=8y$ , we get,
$\dfrac{d{{x}^{2}}}{dx}=\dfrac{d\left( 8y \right)}{dx}$ ………………………(3)
We know the formula, $\dfrac{d{{x}^{n}}}{dx}=n{{x}^{n-1}}$ ……………………(4)
Using this formula and simplifying equation (3), we get
$\dfrac{d{{x}^{2}}}{dx}=\dfrac{d\left( 8y \right)}{dx}$

& \Rightarrow 2{{x}^{n-1}}=8\dfrac{dy}{dx} \\\ & \Rightarrow 2x=8\dfrac{dy}{dx} \\\ & \Rightarrow \dfrac{2x}{8}=\dfrac{dy}{dx} \\\ \end{aligned}$$ $$\Rightarrow \dfrac{x}{4}=\dfrac{dy}{dx}$$ …………………………(5) We know that $$\dfrac{dy}{dx}$$ is a slope which is a tan function. So, $$\dfrac{dy}{dx}=\tan \theta =\dfrac{x}{4}$$ ………………..(6) We have to find the slope of the tangent AB at the point $$\left( 0,0 \right)$$ . So, putting $$\left( 0,0 \right)$$ in equation (6), we get, $$\begin{aligned} & \Rightarrow \dfrac{x}{4}=\tan \theta \\\ & \Rightarrow \dfrac{0}{4}=\tan \theta \\\ \end{aligned}$$ $$\Rightarrow 0=\tan \theta $$ ………………..(7) We know that, $$\tan 0=0$$ ………………….(8) Now, from equation (7) and equation (8), we get $$\tan \theta =\tan 0{}^\circ $$ $$\Rightarrow \theta =0$$ …………………..(9) Now, let us find the slope of the tangent CD of the curve $${{y}^{2}}=8x$$ at the point $$\left( 0,0 \right)$$ . Differentiating with respect to x, the LHS and RHS of the equation of the curve $${{y}^{2}}=8x$$ , we get, $$\dfrac{d{{y}^{2}}}{dx}=\dfrac{d\left( 8x \right)}{dx}$$ Using the chain rule, we can transform it as, $$\Rightarrow \dfrac{d{{y}^{2}}}{dy}\times \dfrac{dy}{dx}=\dfrac{d\left( 8x \right)}{dx}$$ ………………………(10) We know the formula, $$\dfrac{d{{y}^{n}}}{dy}=n{{y}^{n-1}}$$ ……………………(11) Using this formula and simplifying equation (10), we get $$\begin{aligned} & \Rightarrow \dfrac{d{{y}^{2}}}{dy}\times \dfrac{dy}{dx}=\dfrac{d\left( 8x \right)}{dx} \\\ & \Rightarrow 2{{y}^{2-1}}\times \dfrac{dy}{dx}=8 \\\ & \Rightarrow 2y\times \dfrac{dy}{dx}=8 \\\ & \Rightarrow \dfrac{dy}{dx}=\dfrac{8}{2y} \\\ \end{aligned}$$ $$\Rightarrow \dfrac{dy}{dx}=\dfrac{4}{y}$$ …………………………(12) We know that $$\dfrac{dy}{dx}$$ is a slope which is a tan function. So, $$\dfrac{dy}{dx}=\tan \alpha =\dfrac{4}{y}$$ ………………..(13) We have to find the slope of the tangent CD at the point $$\left( 0,0 \right)$$ . So, putting $$\left( 0,0 \right)$$ in equation (13), we get, $$\begin{aligned} & \Rightarrow \dfrac{4}{y}=\tan \alpha \\\ & \Rightarrow \dfrac{4}{0}=\tan \alpha \\\ \end{aligned}$$ $$\Rightarrow \infty =\tan \alpha $$ ………………..(14) We know that, $$\tan \dfrac{\pi }{2}=\infty $$ ………………….(15) Now, from equation (14) and equation (15), we get $$\tan \alpha =\tan \dfrac{\pi }{2}$$ $$\Rightarrow \alpha =\dfrac{\pi }{2}$$ …………………..(16) From equation (9) and equation (16), we have the angle of these tangents from the x-axis. The angle between the tangents CD and AB = $$\alpha -\theta =\dfrac{\pi }{2}-0=\dfrac{\pi }{2}$$ . Therefore, the angle of intersection between the curves $${{x}^{2}}=8y$$ and $${{y}^{2}}=8x$$ at the point $$\left( 0,0 \right)$$ is $$\dfrac{\pi }{2}$$ . Hence, the correct option is (D). Note: In this question, one might think to apply the property that the product of the slope of two perpendicular lines is equal to -1. The slope of the first tangent = $$\dfrac{x}{4}$$ . The slope of the second tangent = $$\dfrac{4}{y}$$ . The product of the slopes of these two tangents = $$\dfrac{x}{4}\times \dfrac{4}{y}=\dfrac{x}{y}$$ …………….(1) We have the coordinate of the point is $$\left( 0,0 \right)$$ . Putting $$\left( 0,0 \right)$$ in equation (1), we get The product of the slopes of these two tangents = $$\dfrac{x}{y}=\dfrac{0}{0}$$ = undefined. Therefore, here we cannot apply the property that the product of the slope of two perpendicular lines is equal to -1.