Question

The angle of incidence for an equilateral prism of refractive index so that the ray is parallel to the base inside the prism is

$A.\,30{}^\circ$
$B.\,20{}^\circ$
$C.\,60{}^\circ$
$D.\,45{}^\circ$
$E.\,75{}^\circ$

Answer 1

This problem can be solved using two methods. Those are, one method is a geometrical method, in which we will draw the ray diagram representing the angle of incidence, the angle of prism and the angle of refraction. The other method is a numerical one, the answer can be found by using Snell’s law formula.
Formula used:
${{n}_{1}}\sin i={{n}_{2}}\sin r$

Complete answer:
From the data, we have the data as follows.
The prism is an equilateral prism, which implies that the angle of the prism is $60{}^\circ$.

Method I: Geometrical method
In this method, we will draw the rays and their related angles.

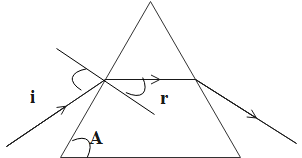
The term ‘i' represents the angle of incidence, the term ‘A’ represents the angle of prism and the term ‘r’ represents the angle of refraction.
As the angle of the prism is $60{}^\circ$, thus, the angle of refraction is given as follows.

& \angle r=90{}^\circ -\angle A \\\ & \Rightarrow \angle r=90{}^\circ -60{}^\circ \\\ & \Rightarrow \angle r=30{}^\circ \\\ \end{aligned}$$ Therefore, the angle of incidence should be equal to the value of $$\angle i=60{}^\circ $$ Method II: Numerical method In this method, we will make use of Snell’s law formula. $${{n}_{1}}\sin i={{n}_{2}}\sin r$$ Where $${{n}_{1}}$$is the incident index, $${{n}_{2}}$$is the refractive index, i is the angle of incidence and r is the angle of refraction. Substitute the given values in the above equation. $$\begin{aligned} & 1\times \sin i=\sqrt{3}\sin 30{}^\circ \\\ & \Rightarrow \sin i=\sqrt{3}\times \dfrac{1}{2} \\\ & \Rightarrow i=60{}^\circ \\\ \end{aligned}$$ As the value of the angle of the incidence equals $$\angle i=60{}^\circ $$. **So, the correct answer is “Option C”.** **Note:** The ray diagram method is easy to understand the given concept visually, but, if asked to solve the problem numerically, then, the numerical method mentioned should be used to solve this problem. Snell’s law formula should be known to solve this type of problem.