Question

The angle of elevation of the top of the tower is ${45^\circ}$ on walking up a slope inclined at an angle of ${30^\circ}$ to the horizontal a distance 20 meters, the angle of elevation of the top of tower is observed to be ${60^\circ}$. The height of the tower is?
A. $10(\sqrt 3 + 1)m$
B. $20(\sqrt 3 + 1)m$
C. $100\sqrt 3 m$
D. $50(3 + \sqrt 3 )m$

Answer 1

According to given in the question we have to find the height of the tower when the angle of elevation of the top of the tower is ${45^\circ}$on walking up a slope inclined at an angle of ${30^\circ}$to the horizontal a distance 20 meters, the angle of elevation of the top of tower is observed to be ${60^\circ}$. So, first of all we have to let the tangent of triangle ABC as given in the figure below:

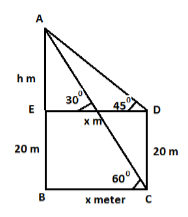
After finding the tangent in triangle ABC by dividing length of sides by length of adjacent sides, Now we have to consider the triangle ADE to find the value of AE = h m and DE = x m. Now, we have to substitute the both the value in the expression as obtained from triangle ABC and now we have to use the rationalization method to find the value of x which is side DE. And hence on substituting the value of x we can obtain the value of h which is the height we want to find.

Formula used: $({a^2} - {b^2}) = (a + b)(a - b)..................(a)$

Complete step-by-step answer:
Given,
Angle of elevation of the top of the tower $= {45^\circ}$
Horizontal distance = 20 units
Slope of inclination $= {30^\circ}$
Observation angle of elevation from the top of the tower $= {60^\circ}$
Step 1: To find the height of the tower h or AE we have to find the tangent of the triangle ABC.
So, tangent of triangle ABC $\tan {60^\circ} = \dfrac{{AB}}{{BC}}$
On substituting the value of AB and BC which are, h + 20 and x,
$\Rightarrow \tan {60^\circ} = \dfrac{{h + 20}}{x}$
Now, as we know that the value of $\Rightarrow \tan {60^\circ} = \sqrt 3$Hence,
$\Rightarrow \sqrt 3 = \dfrac{{h + 20}}{x}$
Step 2: Applying cross-multiplication in step 1.
$\Rightarrow \sqrt 3 x = h + 20.............(1)$
Step 3: Now, we will solve the triangle ADE to obtain the value of x and h.
$\tan {45^\circ} = \dfrac{{AE}}{{DE}} \\\ \tan {45^\circ} = \dfrac{h}{x} \\\$
Now, as we know that the value of $\Rightarrow \tan {45^\circ} = 1$Hence,
$\Rightarrow 1 = \dfrac{h}{x} \\\ \Rightarrow h = x..............(2) \\\$
Step 4: Now, to find the value of x we have to substitute the equation (2) into equation (1) hence,
$\Rightarrow \sqrt 3 x = x + 20 \\\ \Rightarrow \sqrt 3 x - x = 20 \\\ \Rightarrow x = \dfrac{{20}}{{\sqrt 3 - 1}}................(3) \\\$
Step 5: Now, we have to use the rationalization method to find x
$\Rightarrow x = \dfrac{{20}}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}$
To solve the obtained expression just above now we have to apply the formula (a) as mentioned in
the solution hint.

$$\Rightarrow x = \dfrac{{20\sqrt 3 + 1}}{{{{(\sqrt 3 )}^2} - {1^2}}} \\\ \Rightarrow x = \dfrac{{20\sqrt 3 + 1}}{{3 - 1}} \\\ \Rightarrow x = \dfrac{{20\sqrt 3 + 1}}{2} \\\ \Rightarrow x = 10\sqrt 3 + 1 \\\$$

Step 6: Now, to find the value of h we have to substitute the value of x in equation (2)
Hence,
$\Rightarrow h = 10\sqrt 3 + 1$

Final solution: Hence, with the help of the formula (a) and triangle ABC and AED we have obtained the height of the tower which is $h = 10\sqrt 3 + 1m$.

Hence, option (A) is correct.

Note: To find the value of h or the height of tower it is necessary to find the value of tangent in triangle ABC and same as we have to solve the triangle AED.
It is necessary to multiply the inverse of the denominator term with the numerator and
denominator to solve the expression easily.