Question

The angle of elevation of the top of the tower from two points P and Q at distance a and b respectively form the base and in the same straight line with it are complementary. Prove that the height of the tower is$\sqrt {{\text{ab}}}$.

Answer 1

Hint – To prove the height of the tower, we consider the data given in the question and draw a figure which looks like a triangle each from point P and Q respectively. It is given that their angles made to the ground are complementary, i.e. their sum of angles of elevation are 90°. We use properties of triangles to prove height is$\sqrt {{\text{ab}}}$.

Complete step-by-step answer:
Given Data,
Points P and Q are at a distance a and b respectively from the tower. The angles of elevation of P and Q are complementary.
That means if point P makes an angle of elevation θ from the ground, point Q makes an angle of elevation 90° - θ from the ground.
(θ + 90° - θ = 90° -- property of complementary angles)
Now let us draw a figure with all the data given in the question, it looks like:

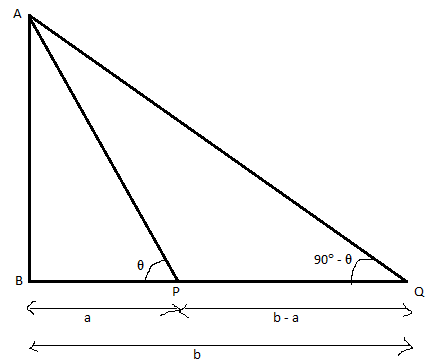
Both the triangles formed are right angles triangles because the tower is placed perpendicular to the ground.
We use the trigonometric properties of triangles,
Now let us consider ∆ABP from the figure,
${\text{Tan }}\theta {\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BP}}}} = \dfrac{{{\text{AB}}}}{{\text{a}}}{\text{ - - - - - }}\left( 1 \right)$
Now let us consider ∆ABQ from the figure,
${\text{Tan }}\left( {90^\circ - \theta } \right){\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BQ}}}}$
We know the trigonometric identity of tan function says, ${\text{Tan }}\left( {90^\circ - \theta } \right) = {\text{Cot }}\left( \theta \right){\text{ and Tan }}\left( \theta \right) = \dfrac{1}{{{\text{Cot }}\left( \theta \right)}}$
Therefore our equation becomes,
$\Rightarrow {\text{Tan }}\left( {90^\circ - \theta } \right){\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BQ}}}} \\\ \Rightarrow {\text{Cot }}\left( \theta \right){\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BQ}}}} \\\ \Rightarrow \dfrac{1}{{{\text{Tan }}\theta }}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BQ}}}} \\\ \Rightarrow {\text{Tan }}\theta {\text{ = }}\dfrac{{{\text{BQ}}}}{{{\text{AB}}}} = \dfrac{{\text{b}}}{{{\text{AB}}}}{\text{ - - - - - }}\left( 2 \right) \\\$
Now comparing equations (1) and (2), we get
$\Rightarrow \dfrac{{{\text{AB}}}}{{\text{a}}} = \dfrac{{\text{b}}}{{{\text{AB}}}} \\\ \Rightarrow {\text{A}}{{\text{B}}^2} = {\text{ab}} \\\ \Rightarrow {\text{AB = }}\sqrt {{\text{ab}}} \\\$
Therefore the height of the tower is$\sqrt {{\text{ab}}}$.
Hence proved.

Note – In order to solve this type of question the key is to know the definition of complementary angles, this gives us the angles of elevation. Anytime there is a question of this type, carefully drawing an appropriate figure helps us easily solve the problem. Having good knowledge in the trigonometric properties of triangles, tangent and cotangent functions and their conversions are essential to establish a relation between both the angles of elevation.
Complementary angles – sum of the angles is 90°.
Supplementary angles – sum of the angles is 180°.