Question

The angle of elevation of the top of the pillar at any point A on the ground is $15{}^\circ$ . On walking 100 ft towards the pillar the angle becomes $30{}^\circ$ . Then height of pillar is
(a) $50\left( 2+\sqrt{3} \right)$
(b) 50
(c) $100\left( 2+\sqrt{3} \right)$
(d) $100\left( 2-\sqrt{3} \right)$

Answer 1

Hint: First, we will assume the height of the pillar to be h. Then we will draw figures to get a better understanding.

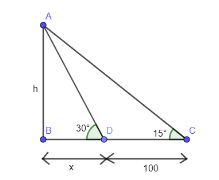
We will first find the value of x by using the trigonometric rule $\tan \theta =\dfrac{opposite}{adjacent}$ in $\Delta ADB$ . Then, we will use this in $\Delta ACB$ . On solving this equation, we will get the equation in root form. So, to remove that we will use conjugate of the number which will be easy to solve. Also, we will use $\tan 15{}^\circ =\tan \left( 45{}^\circ -30{}^\circ \right)$ and will apply the formula $\tan \left( a-b \right)=\dfrac{\tan a-\tan b}{1+\tan a\tan b}$ . Thus, on solving we will get the value of h.

Complete step-by-step answer:

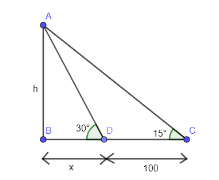
Here, AB is a pillar considered as h. CD is 100 ft as mentioned in question. We have assumed the remaining distance BD as x. So, total length BC is equal to
$BC=BD+DC=x+100$ ………………………………(1)
Now, taking $\Delta ADB$ and using trigonometric rule i.e. $\tan \theta =\dfrac{opposite}{adjacent}$ we get
$\tan \theta =\dfrac{opposite}{adjacent}$
$\tan 30{}^\circ =\dfrac{AB}{BD}=\dfrac{h}{x}$
We know the value of $\tan 30{}^\circ$ is $\dfrac{1}{\sqrt{3}}$ so, on substituting this values, we get
$\dfrac{1}{\sqrt{3}}=\dfrac{h}{x}$
Now, making x as subject, we will get equation as
$x=h\sqrt{3}$ …………………………..(2)
Similarly, we will take $\Delta ACB$ and applying the rule $\tan \theta =\dfrac{opposite}{adjacent}$ , we get
$\tan 15{}^\circ =\dfrac{AB}{BC}$
We can write $\tan 15{}^\circ =\tan \left( 45{}^\circ -30{}^\circ \right)$ and substituting values of AB and BC, we get
$\tan \left( 45{}^\circ -30{}^\circ \right)=\dfrac{h}{x+100}$
Here, we will the formula of $\tan \left( a-b \right)=\dfrac{\tan a-\tan b}{1+\tan a\tan b}$ where a is $45{}^\circ$ and b is $30{}^\circ$ . On substituting this formula, we get equation as
$\dfrac{\tan 45{}^\circ -\tan 30{}^\circ }{1+\tan 45{}^\circ \tan 30{}^\circ }=\dfrac{h}{x+100}$
Now, we know that value of $\tan 45{}^\circ =1$ and $\tan 30{}^\circ$ is $\dfrac{1}{\sqrt{3}}$ so, on putting this we will get
$\dfrac{1-\dfrac{1}{\sqrt{3}}}{1+1\left( \dfrac{1}{\sqrt{3}} \right)}=\dfrac{h}{x+100}$
On further solving, we get
$\dfrac{\dfrac{\sqrt{3-}1}{\sqrt{3}}}{\dfrac{\sqrt{3}+1}{\sqrt{3}}}=\dfrac{h}{x+100}$
Now, we cancel the denominator term as it is common. So, we will get
$\dfrac{\sqrt{3}-1}{\sqrt{3}+1}=\dfrac{h}{x+100}$
Now, we will multiply LHS side with the numerator term i.e. $\sqrt{3}-1$ to remove the root sign. So, we can write
$\dfrac{\sqrt{3}-1}{\sqrt{3}+1}\times \dfrac{\sqrt{3}-1}{\sqrt{3}-1}=\dfrac{h}{x+100}$
On solving, we get
$\dfrac{{{\left( \sqrt{3}-1 \right)}^{2}}}{\left( \sqrt{3}+1 \right)\left( \sqrt{3}-1 \right)}=\dfrac{h}{x+100}$
Using the formula $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ So, we will get
$\dfrac{{{\left( \sqrt{3}-1 \right)}^{2}}}{{{\left( \sqrt{3} \right)}^{2}}-{{\left( 1 \right)}^{2}}}=\dfrac{h}{x+100}$
On simplifying, we get
$\dfrac{{{\sqrt{3}}^{2}}-2\sqrt{3}+1}{3-1}=\dfrac{h}{x+100}$ using the formula ${{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$
Further we get equation as
$\dfrac{4-2\sqrt{3}}{2}=\dfrac{h}{x+100}$
Taking 2 common from LHS side and putting value of x in RHS from equation (2), we get
$2-\sqrt{3}=\dfrac{h}{h\sqrt{3}+100}$
On cross multiplying, we get equation as
$\left( 2-\sqrt{3} \right)\left( h\sqrt{3}+100 \right)=h$
On solving we get
$2\sqrt{3}h+200=h+3h+100\sqrt{3}$
$2\sqrt{3}h+200=4h+100\sqrt{3}$
Now, taking h terms on one side and constant term on other side, so we get
$200-100\sqrt{3}=4h-2\sqrt{3}h$
$100\left( 2-\sqrt{3} \right)=2h\left( 2-\sqrt{3} \right)$
On cancelling the terms, we get
$100=2h$
Dividing the equation by 2, we get
$h=\dfrac{100}{2}=50$
Thus, the height of pillar AB is 50 ft.
Option (b) is the correct answer.

Note: Remember, in this type of problem figure is must. Otherwise this problem cannot be solved. Students sometimes makes mistake in understanding this line i.e. The angle of elevation of the top of the pillar at any point A on the ground is $15{}^\circ$ . On walking 100 ft towards the pillar the angle becomes $30{}^\circ$ . By this they consider base value as 100 ft. And then applying $\tan \theta =\dfrac{opposite}{adjacent}$ answer will be obtained which will be wrong. So, do understand the line and draw the figure accordingly.