Question

The angle of elevation of the top of a vertical tower from two points at distances $a$ and $b$ $(a > b)$ from the base and in the same line with it, are complimentary. If $\theta$ is the angle subtended at the top of the tower by the line joining these points, then $\sin \theta$ is equal to
A. $\dfrac{{a + b}}{{a - b}}$
B. $\dfrac{{a - b}}{{a + b}}$
C. $\dfrac{{(a - b)b}}{{a + b}}$
D. $\dfrac{{a - b}}{{(a + b)b}}$

Answer 1

Hint : As we can see that in the above question we have to find the value of $\sin \theta$ which means that there is use of trigonometric application and identities to get the required answer. We will first draw the diagram according to the data given in the question . We will assume one of the angles as $\phi$ as it cannot be $\theta$ because it is the angle subtended at the top of the tower by the line joining the points.

Complete step-by-step answer :
Let us first draw the diagram according to the question:

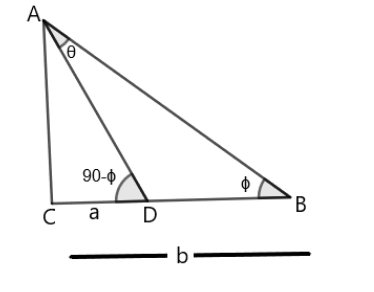
In the above figure we have $\angle BAD = \theta$ ( $\theta$ is the angle subtended at the top of the tower by the line joining these points).
Let us assume $\angle CBA = \phi ,\angle ADC = 90 - \phi$ . Also we have $CD = a$ and $BC = b$ .
Now in triangle CAD , we have $\tan \phi$ , so we have $\tan \phi = \dfrac{p}{b}$ , here the perpendicular is AC and the base is $BC = b$ . So by putting the value we can write $\tan \phi = \dfrac{{AC}}{b}$ .
Again in triangle CAD we can write $\tan (90 - \phi ) = \dfrac{{AC}}{a}$ .
Now we know that $\tan (90 - \theta ) = \cot \theta$ , so it can be written as $\cot \phi = \dfrac{{AC}}{a}$ .
We know the trigonometric identity that $\cot \theta = \dfrac{1}{{\tan \theta }}$ , so by this we can write from the above expressions , $\dfrac{{AC}}{a} = \dfrac{1}{{\dfrac{{AC}}{b}}} \Rightarrow \dfrac{{AC}}{a} = \dfrac{a}{{AC}}$ .
By cross multiplication it can be written as $A{C^2} = ab$ or $AC = \sqrt {ab}$ .
Now we can write $\sin \phi = \dfrac{p}{h}$ , here we have perpendicular is $AC = \sqrt {ab}$ and hypotenuse $AB$ can be written as $A{C^2} + B{C^2}$ , we have $AC = \sqrt {ab}$ and $BC = b$ .
So we have hypotenuse ${h^2} = {(\sqrt {ab} )^2} + {b^2}$, by removing the square of hypotenuse we have i.e. $h = \sqrt {ab + {b^2}}$ .
After putting these values back we have $\sin \phi = \sqrt {\dfrac{{ab}}{{ab + {b^2}}}}$ .
By squaring both the sides we have ${\sin ^2}\phi = {\left( {\sqrt {\dfrac{{ab}}{{ab + {b^2}}}} } \right)^2}$ . Since squaring the square root removes it, we have $\dfrac{{ab}}{{ab + {b^2}}}$ . We can take the common factor out in the denominator, so we have $\dfrac{{ab}}{{b(a + b)}} = \dfrac{a}{{a + b}}$ .
From the above figure and by applying trigonometric identity we can write $\sin \theta = - 1 + 2{\sin ^2}\phi$ .
By putting the value in the identity we have $- 1 + \dfrac{{2a}}{{a + b}}$ , On solving we have $\dfrac{{ - a - b + 2a}}{{a + b}} \Rightarrow \dfrac{{a - b}}{{a + b}}$ .
Hence the correct option is (b) $\dfrac{{a - b}}{{a + b}}$ .
So, the correct answer is “Option B”.

Note : We should note that in the above solution we have used the trigonometric identity that $\sin \theta = - \sin \left( {90 - \phi } \right) = - \cos 2\phi$ . Then there is another identity which says that $\cos 2\theta$ can be written as $1 - 2{\sin ^2}\theta$ , so we can write here $- \cos 2\phi = - 1 + 2{\sin ^2}\phi$ . In triangle CAD we have perpendicular $= AC$ and base $= a$ .