Question

The angle of elevation of the top of a vertical tower from a point P on the horizontal ground was observed to be $\alpha$. After moving a distance of 2 meters from P towards the foot of the tower, the angle of elevation changes to $\beta$. Then the height (in meters) of the tower is:
(A) $\dfrac{{\cos \left( {\beta - \alpha } \right)}}{{\sin \alpha \sin \beta }}$ (B) $\dfrac{{2\sin \left( {\beta - \alpha } \right)}}{{\sin \alpha \sin \beta }}$ (C) $\dfrac{{2\sin \alpha \sin \beta }}{{\sin \left( {\beta - \alpha } \right)}}$ (D) $\dfrac{{\sin \alpha \sin \beta }}{{\cos \left( {\beta - \alpha } \right)}}$

Answer 1

Hint: Analyze the situation with a diagram. Use trigonometric ratios to find the distance of point P from the foot of the tower in both cases. And then compare both values to get the desired result.

Complete step-by-step answer:

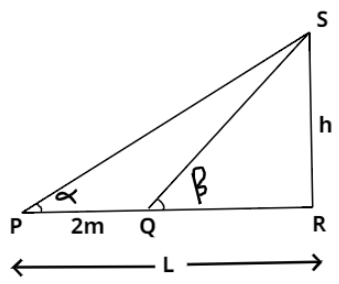
Consider the above figure, let L be the initial distance of the foot of the tower from point P and h be the height of the tower.
As per the information given in the question, $\alpha$ is the angle of elevation of the top of the tower from point P.
From $\Delta PRS$ shown above:
$\Rightarrow \tan \alpha = \dfrac{{SR}}{{PR}} \\\ \Rightarrow \tan \alpha = \dfrac{h}{L} \\\ \Rightarrow L = \dfrac{h}{{\tan \alpha }} .....(i) \\\$
Now, after moving 2 meters towards the tower we reach another point Q. Then the distance between the foot of the tower and point Q is $L - 2$. And the angle of elevation of the top of the tower from point Q is given in the question as $\beta$. So in $\Delta QSR$ in the above figure:
$\Rightarrow \tan \beta = \dfrac{{SR}}{{QR}} \\\ \Rightarrow \tan \beta = \dfrac{h}{{L - 2}}, \\\ \Rightarrow L - 2 = \dfrac{h}{{\tan \beta }}, \\\ \Rightarrow L = \dfrac{h}{{\tan \beta }} + 2 .....(ii) \\\$
Now, comparing equation $(i)$ and $(ii)$, we have:
$\Rightarrow \dfrac{h}{{\tan \alpha }} = \dfrac{h}{{\tan \beta }} + 2, \\\ \Rightarrow h\left( {\dfrac{1}{{\tan \alpha }} - \dfrac{1}{{\tan \beta }}} \right) = 2, \\\$
Taking $\tan \alpha \tan \beta$ as LCM, we’ll get:
$\Rightarrow h\left( {\dfrac{{\tan \alpha - \tan \beta }}{{\tan \alpha \tan \beta }}} \right) = 2, \\\ \Rightarrow h = \dfrac{{2\tan \alpha \tan \beta }}{{\tan \alpha - \tan \beta }} \\\$
Now we know that, $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$, applying this we’ll get:

$$\Rightarrow h = \dfrac{{2 \times \dfrac{{\sin \alpha }}{{\cos \alpha }} \times \dfrac{{\sin \beta }}{{\cos \beta }}}}{{\dfrac{{\sin \alpha }}{{\cos \alpha }} - \dfrac{{\sin \beta }}{{\cos \beta }}}}, \\\ \Rightarrow h = \dfrac{{2 \times \dfrac{{\sin \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}}{{\dfrac{{\sin \alpha \cos \beta - \cos \alpha \sin \beta }}{{\cos \alpha \cos \beta }}}}, \\\ \Rightarrow h = \dfrac{{2\sin \alpha \sin \beta }}{{\sin \alpha \cos \beta - \cos \alpha \sin \beta }} \\\$$

We know that, $\sin A\cos B - \cos A\sin B = \sin \left( {A - B} \right)$, applying this formula, we’ll get:
$\Rightarrow h = \dfrac{{2\sin \alpha \sin \beta }}{{\sin \left( {\alpha - \beta } \right)}}$
Therefore, the height of the tower is $\dfrac{{2\sin \alpha \sin \beta }}{{\sin \left( {\alpha - \beta } \right)}}$. Option (C) is correct.
Note: We can use any of the trigonometric ratios to get the end results. But in this case, perpendicular and base are known for the given angles so it is convenient to use either $\tan \theta {\text{ or }}\cot \theta$. If we want to use any other trigonometric ratios, then we have to determine hypotenuse first by using Pythagoras theorem.