Question
Question: The angle of elevation of the top of a tower at a distance \(500\) meters from the foot is \({30^\ci...
The angle of elevation of the top of a tower at a distance 500 meters from the foot is 30∘. The height of the tower is-
A.2503 meters
B.3500 meters
C.5003 meters
D.250 meters
Solution
Assume the height of the tower to be AB= h. Then we can use the formula of trigonometric ratio-
⇒tanθ=BP where P is the perpendicular and B is the base of the triangle. Put the value of θ=30∘, P=AB and B=BC. Now, we know that tan30∘=31 . Put this value and the value of AB and BC in the formula and solve it for h.
Complete step-by-step answer:
Given the angle of elevation of the top of the tower at any point in groundθ=30∘
The distance of the foot of the tower from that point in ground is =500 meters
We have to find the height of the tower.
Let us assume that the tower is AB and let the point on the ground be C. And let the height of the tower be h meter.
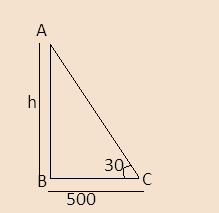
Here, ∠ACB=30∘ and ∠ABC=90∘
AB=h and BC=500 meters
Now in △ABC,
⇒tanθ=BCAB as AB is the perpendicular here and BC is the base.
On putting the given values we get-
⇒tan30∘=500h
Now we know that the value of tan30∘=31
Then on putting this value, we get-
⇒31=500h
On cross multiplication, we get-
⇒500=h3
We can also write it as-
⇒h3=500
On solving for h, we get-
⇒h=3500 meters
Hence the height of the tower is3500 meters
The correct answer is B.
Note: Here we have not used the formula of sine ratio or cosine ratio because we do not know the value of the hypotenuse in the triangle formed. And we know that sine and cosine ratios are given as-
⇒sinθ=HP and cosθ=HB where P is perpendicular, B is base and H is hypotenuse of the triangle.
Since we do not know the value of hypotenuse we cannot solve the equation further to get the value of the height of the tower h.
