Question

The angle of elevation of the top of a flag post from a point on a horizontal ground is found to be ${30^o}$. On walking 6m towards the post, the elevation increased by ${15^o}$. Find the height of the flag post.

Answer 1

Here we will first draw the figures for the question and then use trigonometric relation for a triangle.

Complete step by step solution:
The angle of elevation of the top of a flag post from a point on a horizontal ground is found to be ${30^o}$ and after walking 6m towards the post, the elevation increased by ${15^o}$.

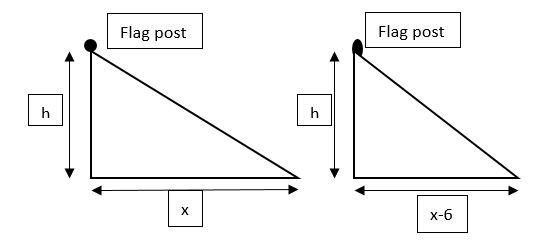
In the first triangle, angle of elevation of the top of a flag post from a point on a horizontal ground is ${30^o}$ and in second triangle, angle of elevation of the top of a flag post from a point on a horizontal ground is ${30^o} + {15^o}$ that is, ${45^0}$.
Let the height of the flag post be “h”
Let, point on a horizontal ground for the first triangle is x m away from the flag post position, then, point on a horizontal ground for the second triangle will be $x - 6$ m away from the flag post position because walked $6m$ towards the post.
For first triangle: $\tan {30^o} = \frac{{Perpendicular}}{{Base}} = \frac{h}{x}$
$\frac{1}{{\sqrt 3 }} = \frac{h}{x}$
$x = \sqrt 3 h$……….(1)
For first triangle: $\tan {45^o} = \frac{{Perpendicular}}{{Base}} = \frac{h}{{x - 6}}$
$1 = \frac{h}{{x - 6}}$
$x - 6 = h$………(2)
Substituting value of x from equation 1 in equation 2:
$\sqrt 3 h - 6 = h$
$\left( {\sqrt 3 - 1} \right)h = 6$
$h = \frac{6}{{\sqrt 3 - 1}} = 8.19m$

Hence, height of flag post is $8.19$m

Note: It is easy to solve this kind of question by drawing the figure to visualize and solve.