Question

The angle of elevation of the sun, if the length of the shadow of the tower is $\dfrac{1}{{\sqrt 3 }}$ times the height of the tower is:
A) ${30^ \circ }$
B) ${75^ \circ }$
C) ${60^ \circ }$
D) ${45^ \circ }$

Answer 1

The given question belongs to the height and distances concept of trigonometry domain. In the problem, we are given the relation between the heights of the shadow and the tower. So, we first draw a figure to represent the situation and understand the problem more clearly. We introduce some variables for the length of shadow and height of the tower and form a relation between them. Then, we find the final answer using the definition of the trigonometric functions.

Complete step by step solution:
Let us assume the height of the tower as $x$ meters.
Then, the length of the shadow of the tower $= \dfrac{x}{{\sqrt 3 }}$ metres
So, the situation can be represented as in the figure below:

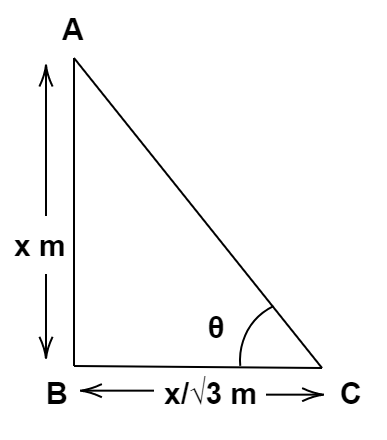
Here, theta is the angle of elevation of the sun.
In triangle ABC, we have assumed the angle of elevation of the sun, that is $\angle ACB$ as $\theta$. We also have represented the height of the tower and its shadow in terms of a variable x.
Now, the tangent of the angle $\theta$ is equal to $\dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}}$. So, in triangle ABC, we get,
$\Rightarrow \tan \theta = \dfrac{{x \,\,m}}{{\left( {\dfrac{x}{{\sqrt 3 }}} \right)\,m}}$
Now, cancelling the common terms in numerator and denominator, we get,
$\Rightarrow \tan \theta = \dfrac{1}{{\left( {\dfrac{1}{{\sqrt 3 }}} \right)}} = \sqrt 3$
Now, we know that the tangent of the angle ${60^ \circ }$ is equal to $\sqrt 3$. Hence, we have,
$\theta = {60^ \circ }$
Therefore, the angle of elevation of the sun is ${60^ \circ }$. Hence, option (C) is the correct answer.

Note:
The definition of the tangent function in terms of the sides of a right angled triangle must be known so as to form a relation between the angle and the sides of the triangle. Also, the value of the trigonometric functions must be known at some standard angles such as ${30^ \circ }$, ${45^ \circ }$, ${60^ \circ }$, and ${90^ \circ }$. The simplification of division of two rational numbers must be known in order to simplify the value and get to the final answer.