Solveeit Logo
Login

Question

Question: The angle of elevation of an electric pole from a point A to the ground is 60° and from a point B to...

The angle of elevation of an electric pole from a point A to the ground is 60° and from a point B towards the pole on the line joining the foot of the pole to the point is 75°. If the distance AB = a, then the height of the pole is :
A.a(3+23)2\dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}
B.a(4+23)a\left( {4 + 2\sqrt 3 } \right)
C.a(2+3)2\dfrac{{a\left( {2 + \sqrt 3 } \right)}}{2}
D.a(23−3)2\dfrac{{a\left( {2\sqrt 3 - 3} \right)}}{2}

Explanation

Solution

We will first draw the figure of the given condition and then we will use the formula of tan⁡θ=perpendicularbase\tan \theta = \dfrac{{perpendicular}}{{base}} in both the given angles of tan using the formula of tan(a+b) = tan⁡a+tan⁡b1−tan⁡atan⁡b\dfrac{{\tan a + \tan b}}{{1 - \tan a\tan b}} and then from the obtained two equations, we will determine the value of height.

Complete step-by-step answer:
We are given the angle of elevation of an electric pole from a point A from the ground is given as 60° .
Also, the angle of elevation made by point B from the line joining the foot of the pole is 75°.
We are given the distance between the points A and B is AB = a.
Let us draw the figure:

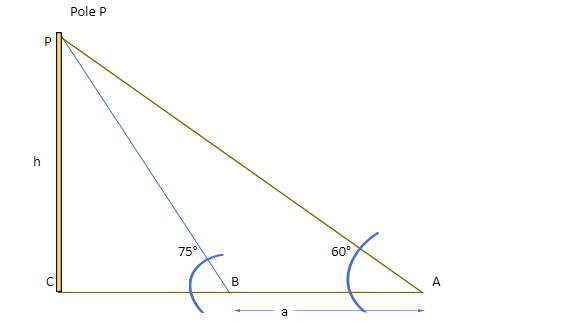
let us assume that distance BC = x
hence, in triangle BCP, tan⁡75∘=hb\tan 75^\circ = \dfrac{h}{b}
Now, tan 75° can be written as tan⁡(45∘+30∘)\tan (45^\circ + 30^\circ )
We can further solve it as tan⁡(45∘+30∘)=tan⁡45∘+tan⁡30∘1−tan⁡45∘tan⁡30∘\tan (45^\circ + 30^\circ ) = \dfrac{{\tan 45^\circ + \tan 30^\circ }}{{1 - \tan 45^\circ \tan 30^\circ }} using the formula tan (a + b) = tan⁡a+tan⁡b1−tan⁡atan⁡b\dfrac{{\tan a + \tan b}}{{1 - \tan a\tan b}}.
⇒tan⁡(45∘+30∘)=1+131−1(13) ⇒tan⁡75∘=3+13−1=(3+1)(3+1)3−1=3+1+232=2(2+3)2=(2+3)  \Rightarrow \tan ({45^ \circ } + {30^ \circ }) = \dfrac{{1 + \dfrac{1}{{\sqrt 3 }}}}{{1 - 1(\dfrac{1}{{\sqrt 3 }})}} \\\ \Rightarrow \tan {75^ \circ } = \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 - 1}} = \dfrac{{\left( {\sqrt 3 + 1} \right)\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} = \dfrac{{3 + 1 + 2\sqrt 3 }}{2} = \dfrac{{2\left( {2 + \sqrt 3 } \right)}}{2} = \left( {2 + \sqrt 3 } \right) \\\
Therefore, tan75∘^ \circ = hb=(2+3)\dfrac{h}{b} = \left( {2 + \sqrt 3 } \right)
⇒b=h2+3\Rightarrow b = \dfrac{h}{{2 + \sqrt 3 }}
Now, in triangle ACP, tan 60∘^ \circ = ha+b\dfrac{h}{{a + b}}
Substituting the values of b and tan 60∘^ \circ , we get
⇒3=ha+b ⇒h=3(a+b) ⇒h=3(a+h2+3) ⇒h−h32+3=a3 ⇒h(2+3−32+3)=a3  \Rightarrow \sqrt 3 = \dfrac{h}{{a + b}} \\\ \Rightarrow h = \sqrt 3 \left( {a + b} \right) \\\ \Rightarrow h = \sqrt 3 \left( {a + \dfrac{h}{{2 + \sqrt 3 }}} \right) \\\ \Rightarrow h - \dfrac{{h\sqrt 3 }}{{2 + \sqrt 3 }} = a\sqrt 3 \\\ \Rightarrow h\left( {\dfrac{{2 + \sqrt 3 - \sqrt 3 }}{{2 + \sqrt 3 }}} \right) = a\sqrt 3 \\\
Simplifying it further for the value of h, we get
∴h=a(3+23)2\therefore h = \dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}
Therefore, the height of the pole h is found to be a(3+23)2\dfrac{{a\left( {3 + 2\sqrt 3 } \right)}}{2}

Note: You should not get confused while calculating the tan75∘^ \circ with tan45∘^ \circ + tan30∘^ \circ instead of tan(45∘^ \circ + tan30∘^ \circ ). Be careful while simplifying for h because there are further calculations based on h value. If h value is wrong the final answer will come wrong.