Question

The angle of elevation of a tower from a point on the same level as the foot of the tower is ${30^ \circ }$ on advancing $150$ meters towards the foot of the tower, the angle of elevation of the tower increases to ${60^ \circ }$ . Find the height of the tower.
a) $50(\sqrt 3 + 1)$
b) $50(\sqrt 3 - 1)$
c) $75\sqrt 3$
d) None of these

Answer 1

Hint : The question is from the applications of trigonometry. We are given with some angles and distance and are asked to find the height by using trigonometry. We will use different trigonometric operations to find out the height of the tower. After drawing the diagram we will find out the unknown sides by using different trigonometric ratios.
From the basics of trigonometric ratios we have:
$\tan \theta = \dfrac{{perpendicular}}{{base}}$

Complete step-by-step answer :
Let’s first draw the required triangle that will be needed to solve the given question
-
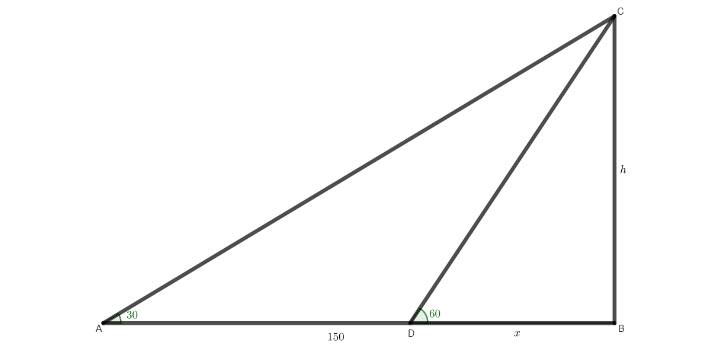Here, we have $AD = 150$ m
And let’s take $DB = x$ m
Here we have $\angle ABC$ right angled triangle, hence we have $ABC$ as a right angled triangle
So, $DBC$ is also a right angled triangle
Now, we have
$\dfrac{{CB}}{{BD}} = \tan {60^ \circ } = \sqrt 3$
Now, we have $CB = h$
And $DB = x$
So by putting this values in the above equation
We get the following:
$\dfrac{h}{x} = \sqrt 3$
Now by cross multiplication we have
$x = \dfrac{h}{{\sqrt 3 }}$ --(1)
Now in the right angle triangle $ABC$ ,we have
$\dfrac{{BC}}{{AB}} = \tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}$
Now we have $CB = h$ and $AB = (x + 150)$ m
Hence, now putting this values in the above equation we get:
$\dfrac{h}{{x + 150}} = \dfrac{1}{{\sqrt 3 }}$
So by cross multiplication we have
$\sqrt 3 h = x + 150$
On putting $x = \dfrac{h}{{\sqrt 3 }}$ from (1) we have:
$\sqrt 3 h = \dfrac{h}{{\sqrt 3 }} + 150$
Now solving the above equation we get:
$\sqrt 3 h - \dfrac{h}{{\sqrt 3 }} = 150$
$\Rightarrow (\sqrt 3 - \dfrac{1}{{\sqrt 3 }})h = 150$
$\Rightarrow (\dfrac{{3 - 1}}{{\sqrt 3 }})h = 150$
$\Rightarrow \dfrac{2}{{\sqrt 3 }}h = 150$
After cross multiplication we have
$h = 75\sqrt 3$
Hence height is $75\sqrt 3$ m.
So, the correct answer is “Option C”.

Note : While calculating the trigonometric ratio we should take care of the values we are putting because a small change in values may give us a totally different value. Try to put attention in the picture, first draw the picture because half of the solution lies in the picture.