Question

The angle of elevation of a tower from a point on the ground is {\text{30^\circ}}. At a point on the horizontal line passing through the foot of the tower and 100 meters nearer to it. If the angle of elevation is found to be {\text{60^\circ }}, then height of the tower is
A. ${\text{50}}\sqrt {\text{3}}$meters
B. $\dfrac{{{\text{50}}}}{{\sqrt {\text{3}} }}$meters
C. ${\text{100}}\sqrt {\text{3}}$meters
D. $\dfrac{{{\text{100}}}}{{\sqrt {\text{3}} }}$meters

Answer 1

We can draw a figure with the details given in the question. We can assume the height of the tower to be h and the distance from the foot of the tower to the 1st point to be x. Then the distance to the 2nd point will be 100-x. Then we can find two right triangles and we can find 2 trigonometric ratios with the given angles which gives a relation of the height h with the base of the triangles. We have 2 equations with h and x. we can substitute for x in one equation and solve for h to get the height.

Complete step by step Answer:

Firstly, we need to draw a figure based on the given information.

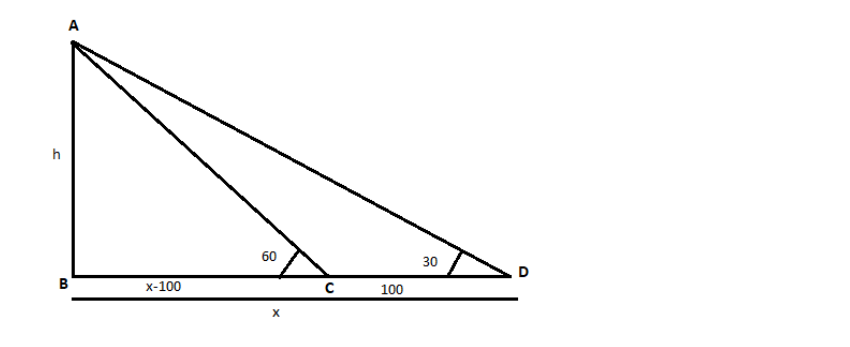
Here the height of the tower is h and the distance from the base of the tower to the point D is x, and given that CD is 100m, therefore ${\text{BC = BD - CD = x - 100m}}$,
Consider triangle ABC,
${\text{tanC = }}\dfrac{{{\text{AB}}}}{{{\text{BC}}}}$
$\Rightarrow {\text{tan6}}{{\text{0}}^{\text{o}}}{\text{ = }}\dfrac{{\text{h}}}{{{\text{x - 100}}}}$
On substituting the value of ${\text{tan6}}{{\text{0}}^{\text{o}}}{\text{ = }}\sqrt {\text{3}}$, we get,
$\sqrt {\text{3}} {\text{ = }}\dfrac{{\text{h}}}{{{\text{x - 100}}}}$ …. (1)
Consider triangle ABD,
${\text{tanD = }}\dfrac{{{\text{AB}}}}{{{\text{BD}}}}$
$\Rightarrow {\text{tan3}}{{\text{0}}^{\text{o}}}{\text{ = }}\dfrac{{\text{h}}}{{\text{x}}}$
On substituting the value of ${\text{tan3}}{{\text{0}}^{\text{0}}}{\text{ = }}\dfrac{{\text{1}}}{{\sqrt {\text{3}} }}$, we get,
$\dfrac{{\text{1}}}{{\sqrt {\text{3}} }}{\text{ = }}\dfrac{{\text{h}}}{{\text{x}}}$
On rearranging, we get,
${\text{x = h}}\sqrt {\text{3}}$ …… (2)
substituting equation (2) in (1), we get,
$\sqrt {\text{3}} {\text{ = }}\dfrac{{\text{h}}}{{{\text{h}}\sqrt {\text{3}} {\text{ - 100}}}}$

$${\text{3h - 100}}\sqrt {\text{3}} {\text{ = h}} \\\ \Rightarrow {\text{2h = 100}}\sqrt {\text{3}} \\\ \Rightarrow {\text{h = }}\dfrac{{{\text{100}}}}{{\text{2}}}\sqrt {\text{3}} {\text{ = 50}}\sqrt {\text{3}} {\text{m}} \\\$$

So, height of the tower is ${\text{50}}\sqrt {\text{3}}$meters
Therefore, the correct answer is option A.
Note: The concept of trigonometry is used. In this problem, we have 2 unknowns. So, we need two 2 equations to solve 2 unknowns. Thus, we form 2 trigonometric equations from the given data. We don’t need to solve for the other variable as it is asked in the question. We must also understand that the angle of elevation increases as we move towards the tower. We must read the question keeping this in mind so that we don’t make mistakes while taking the height and In this question, the ratio between the two non-hypotenuse sides of the triangle is needed. So, we take the tan of the angle to get the ratio. We must also understand tan is the ratio of the length of the opposite side to the adjacent side of the right-angled triangle.