Question

The angle of elevation of a tower from a point 150 m away from the foot of the tower is ${60^ \circ }$. Find the height of the tower.

Answer 1

First of all we will create a figure using the data given. Now, we will just have to find the trigonometric ratio such that it contains the given distance and height, we need to find and then by putting in the values, we will get the answer.

Complete step-by-step answer:
Let us first draw the figure. Let AB be the tower and C be the point which is 150 m distant from the tower. So, we will get the figure a given below:-

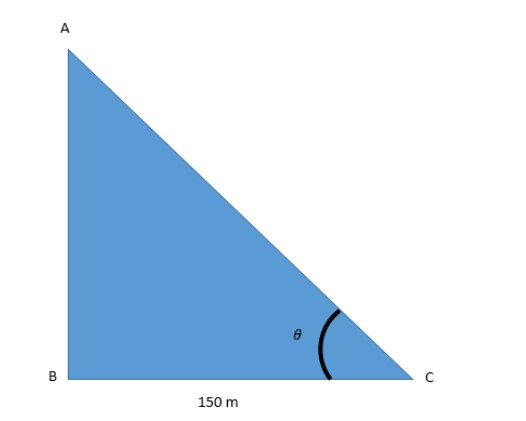
We know that $\tan \theta = \dfrac{{Perpendicular}}{{Base}}$.
Here the perpendicular will be AB and base will be AC.
So, we will get:-
$\tan {60^ \circ } = \dfrac{{AB}}{{BC}}$ ……….(1)
We also know that $\tan {60^ \circ } = \sqrt 3$ …….(2)
Putting in AB = 150 m (because it is given that the distance of point from tower is 150 m) and (2) in equation (1), we will get:-
$\sqrt 3 = \dfrac{{AB}}{{150}}$
Cross multiplying it, to get as follows:-
$AB = 150\sqrt 3 m$.
Hence, the height of the tower is $150\sqrt {30} m$.

Note: Drawing a figure gives us a clearer picture to see what is given in the question because you may put in the wrong values of the perpendicular and base, which will eventually lead to a wrong answer.And If the tangent ratio of an angle is equal to 1, that means that the length of the opposite side equals the length of the adjacent side.