Question

The angle of elevation of a tower at a point is ${45^ \circ }$.After going 40m towards the foot of the tower,the angle of elevation of the tower is ${60^ \circ }$.Find the height of the tower.

Answer 1

Using the given data ,sketch the diagram with AC as the tower and B is the point from where the angle of elevation is measured initially. From this , $\tan {45^ \circ } = \dfrac{{AC}}{{AB}}$
And calculating further we get $40 + x = h$ and we are said that the point moves 40m further and the angle of elevation there is ${60^ \circ }$ and once again calculating $\tan {60^ \circ } = \dfrac{h}{x}$we get $\sqrt 3 x = h$ and simplifying further we get the height of the tower.

Complete step-by-step answer:
Step 1: Lets sketch the diagram with the given details

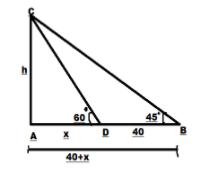
Step 2:Here ,in this diagram, AC is the tower and B is the point from where the angle of elevation is measured initially. Therefore the angle of elevation at B is ${45^ \circ }$.
Step 3:It is given that ,when we move 40m towards the tower ,then the angle of elevation is
${60^ \circ }$.Therefore the angle of elevation at D is ${60^ \circ }$ and DB=40 and $AD = x$. From this we get that AB=40+x.

Step 3:Now, from the diagram
$\Rightarrow \tan {45^ \circ } = \dfrac{{AC}}{{AB}}$
Here , we know that $\tan {45^ \circ } = 1$
$\Rightarrow 1 = \dfrac{h}{{40 + x}}$
$\Rightarrow 40 + x = h$……………….(1)
Step 4: Now, let's do the same step with ${60^ \circ }$
$\Rightarrow \tan 60 = \dfrac{h}{x} \\\ \Rightarrow \sqrt 3 = \dfrac{h}{x} \\\$
$\Rightarrow \sqrt 3 x = h$………………..(2)
Step 5:Now let's equate the equations (1) and (2) as the right hand side of both the equations are the same.
$\Rightarrow 40 + x = \sqrt 3 x \\\ \Rightarrow 40 = \sqrt 3 x - x \\\$
Now ,let's take x common in the right hand side
$\Rightarrow 40 = x(\sqrt 3 - 1)$
We know that the value of $\sqrt 3 = 1.732$.So substitute it in the equation above
$\Rightarrow 40 = x(1.732 - 1) \\\ \Rightarrow 40 = x(0.732) \\\ \Rightarrow \dfrac{{40}}{{0.732}} = x \\\ \Rightarrow x = 54.64 \\\$
Step 6:Now using the value of x in equation (2)
$\Rightarrow \sqrt 3 *(54.64) = h \\\ \\\$
As $\sqrt 3 = 1.732$
$\Rightarrow 1.732*54.64 = h \\\ \Rightarrow 94.64 = h \\\$
Therefore the height of the tower is 94.6 m

Note: In these kinds of sums ,the diagram is very important and you may lose marks even if your answer is correct and the diagram is missing.
We need to be careful in marking the angles at the right places.
Many tend to make a mistake by taking AB as 40m.So you need to read the question more carefully.