Question

The angle of elevation of a ladder against a wall is ${{60}^{\circ }}$ and the foot of the ladder is $9.5$ meter away from the wall. Find the length of the ladder.

Answer 1

Hint:First, we will draw the figure with the details given to us. Then, we will use the formula of trigonometric ratios with angles to solve the question. The formula is given by $\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$.

Complete step-by-step answer:
The diagram for the question is shown below.

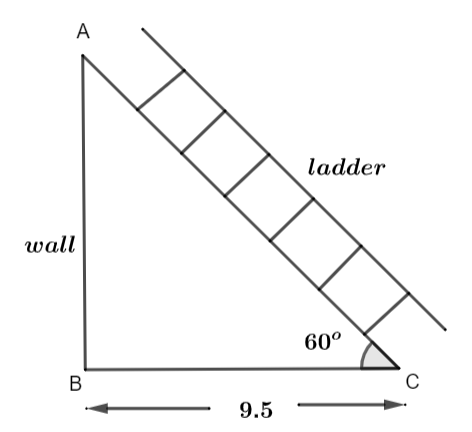
Clearly, AC represents the ladder which is standing against the wall AB. The distance of the bottom of the ladder and the wall is 9.5 meters. We are supposed to find the value of AC that is the length of the ladder.
For that we will apply the trigonometric formula given by $\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$. Since, the angle of elevation of a ladder against a wall is ${{60}^{\circ }}$ therefore the angle $\angle ACB={{60}^{\circ }}$.
Now, we use the formula $\cos \left( \theta \right)=\dfrac{\text{Base}}{\text{Hypotenuse}}$. As we know that the base is BC and the hypotenuse is AC.
Thus, we get $\cos \left( {{60}^{\circ }} \right)=\dfrac{BC}{AC}$ where $\theta ={{60}^{\circ }}$. Since, BC = 9.5 meters.
Therefore, we have $\cos \left( {{60}^{\circ }} \right)=\dfrac{9.5}{AC}$. Now, we will substitute the value of $\cos \left( {{60}^{\circ }} \right)=\dfrac{1}{2}$. This result into, $\begin{aligned} & \dfrac{1}{2}=\dfrac{9.5}{AC} \\\ & \Rightarrow AC=9.5\times 2 \\\ & \Rightarrow AC=19 \\\ \end{aligned}$
Hence, the height of the ladder is 19 meters.

Note: We could have used the trigonometric formula $\tan \left( \theta \right)=\dfrac{\text{perpendicular}}{\text{Base}}$ in the question. Therefore, we get $\tan \left( {{60}^{\circ }} \right)=\dfrac{AB}{BC}$. Since, $\tan \left( {{60}^{\circ }} \right)=\sqrt{3}$ so, we have $\sqrt{3}=\dfrac{AB}{BC}$. Also we can substitute BC = 9.5 meters therefore, we have
$\begin{aligned} & \sqrt{3}=\dfrac{AB}{9.5} \\\ & \Rightarrow \dfrac{AB}{9.5}=\sqrt{3} \\\ & \Rightarrow AB=\sqrt{3}\times 9.5...(iii) \\\ \end{aligned}$
And we have applied $\sin \left( \theta \right)=\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Therefore, we have $\sin \left( {{60}^{\circ }} \right)=\dfrac{AB}{AC}$. Now, we will substitute the value of $\sin \left( {{60}^{\circ }} \right)=\dfrac{\sqrt{3}}{2}$ therefore, we have
$\begin{aligned} & \dfrac{\sqrt{3}}{2}=\dfrac{AB}{AC} \\\ & \Rightarrow AB=\dfrac{\sqrt{3}}{2}\times AC...(iv) \\\ \end{aligned}$
Now, we will equate the equations (iii) and (iv) therefore, we have
$\begin{aligned} & \sqrt{3}\times 9.5=\dfrac{\sqrt{3}}{2}\times AC \\\ & \Rightarrow \sqrt{3}\times 9.5\times \dfrac{2}{\sqrt{3}}=AC \\\ & \Rightarrow AC=\sqrt{3}\times 9.5\times \dfrac{2}{\sqrt{3}} \\\ \end{aligned}$
After cancelling the $\sqrt{3}$ we get
$\begin{aligned} & AC=\sqrt{3}\times 9.5\times \dfrac{2}{\sqrt{3}} \\\ & \Rightarrow AC=9.5\times 2 \\\ & \Rightarrow AC=19 \\\ \end{aligned}$
Hence, the required value of the ladder is 19 meters.