Question
Question: The angle of elevation of a jet plane from a point on the ground is \({{60}^{\circ }}\). After a fli...
The angle of elevation of a jet plane from a point on the ground is 60∘. After a flight of 30 seconds, the angle of elevation changes to 30∘. If the jet plane is flying at a constant height of 36003 m, find the speed of the jet plane.
Solution
Hint: Assume a variable s which will represent the speed of the jet plane in m/s. According to the information given in the question, we can make the figure of the whole situation given in the question. The distance is given by multiplying the speed with the time. Also, from trigonometry, the tan of any angle is given by the ratio of height and the base of the right triangle. Using this, we can solve this question.
Complete step-by-step answer:
Before proceeding with the question, we must know all the formulas that will be required to solve this question.
The distance is given by the product of speed and the time . . . . . . . . . (1)
From trigonometry, the tan of an angle is equal to the ratio of perpendicular height and the base of the triangle . . . . . . . . . . . . (2)
Let us draw the figure according to the information given in the question.
In this question, it is given that the angle of elevation of a jet plane at a point A from a point C on the ground is 60∘. After a flight of 30 seconds, the plane reaches point B and the angle of elevation from point C changes to 30∘. Also, it is given that the height of the plane is constant and is equal to 36003 m. So, we can say that AD = BE = 36003.
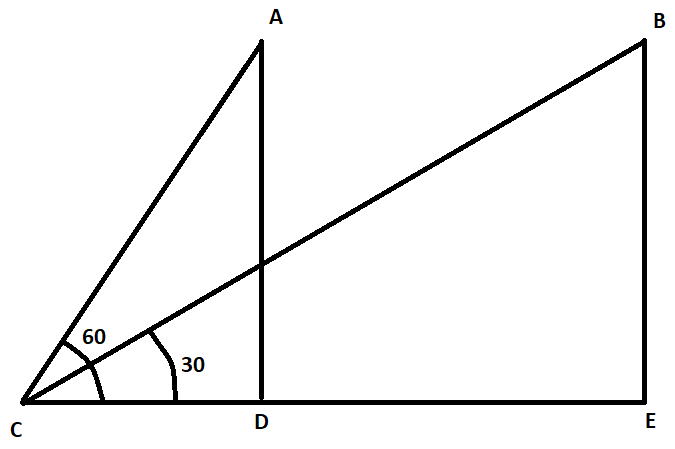
Let us assume that the plane is moving at a speed of s m/s. Since the time of flight is 30 s, from formula (1), the distance AB = DE = 30s.
In triangle ACD, using formula (2) at angle C, we get,
tan60=CDAD⇒CD=tan60AD
Substituting AD = 36003 and tan60=3, we get,
CD=336003⇒CD=3600
In triangle BCE, using formula (2) at angle C, we get,
tan30=CEBE⇒CE=tan30BE⇒CD+DE=tan30BE
Substituting BE = 36003 and tan30=31, CD = 3600 and DE = 30 s, we get,
3600+30s=3136003⇒30s=(3600×3×3)−3600⇒30s=3600(3−1)⇒s=120(2)⇒s=240m/s
Hence, the speed of the jet plane is 240 m/s.
Note: This question is an easy question which can be done if one draws the figure correctly. There is a possibility that one may commit a mistake while drawing the figure. It is possible that one may consider the initial angle of elevation as ∠CAD instead of ∠ACD which will lead us to an incorrect answer.
