Question

The angle of elevation of a cloud from a point of $200{\text{ }}metres$ above a lake is ${30^o}$ and the angle of depression of the reflection of the cloud in the lake is ${60^o}$ . Find the height of the cloud.
A.The height of cloud = 400m
B.The height of cloud = 280m
C.The height of cloud = 340m
D.None of these

Answer 1

Hint : We have given the angle of elevation cloud from the point $200{\text{ }}metres$above the lake is ${30^o}$an angle of depression is of reflection of the cloud is ${60^o}$. So, firstly we have to draw a rough diagram of the situation. After this, we calculate the base length. This base length helps us to find the height of the cloud from the ground level.

Complete step-by-step answer :
Thus is the diagram of the given situation;

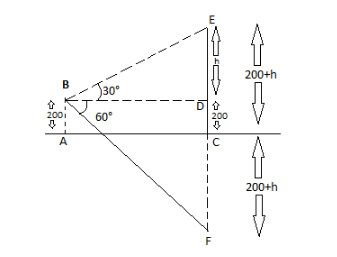
The point is $60m$ above the ground level. We take it as AB.
$AB{\text{ }} = {\text{ }}CD$
$CD{\text{ }} = {\text{ }}200m$
Let $DE{\text{ }} = {\text{ }}h$
So the height of the cloud $= {\text{ }}\left( {200 + h} \right){\text{ }}metre$ . If we calculate the value of h we can find the height of the cloud.
Let BD = $x{\text{ }}metre$ .
Let the reflection of the cloud is at point F. As we know that the distance of the reflection from the ground level is the same as the distance of the object from the ground level. So,
$CF{\text{ }} = {\text{ }}200 + h$
Now from the triangle BDE $\angle D{\text{ }} = {\text{ }}{90^o}$
So triangle BDE is the right-angled triangle; $\tan \theta = \dfrac{{perpendicular}}{{base}}$
∴ $tan{30^o}$ $= \dfrac{h}{x}$
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{x} \Rightarrow x = \sqrt 3 h$ ……………..(i)
In $\Delta {\text{ }}BDF$ , $\angle D = {90^o}$
∴ triangle BDF is the right-angled triangle, therefore $tan{60^o}$ $= \dfrac{{DF}}{{BD}}$
$\Rightarrow \sqrt 3 = \dfrac{{200 + 200 + h}}{x}$
$\sqrt 3 x = 400 + h$ ………….(ii)
From the equations (i) value of $x{\text{ }} =$ $\sqrt 3 h$
Therefore, in (ii)
$\sqrt 3 \left( {\sqrt 3 h} \right) = 400 + h$
$3h = 400 + h$
$3h{\text{ }}-h{\text{ }} = {\text{ }}400$
$2h{\text{ }} = {\text{ }}400$
$h = \dfrac{{400}}{2}$
$= {\text{ }}200m$
So, the value of h $= {\text{ }}200m$
Now we can find the height of cloud
Height of cloud $= {\text{ }}200 + h{\text{ }} = {\text{ }}200 + 200{\text{ }} = {\text{ }}400m$
So, option A is correct.
So, the correct answer is “Option A”.

Note : I.Angle of depression is a downward angle from the horizontal to the line of sight from the observer to some point of interest.
II.The tangent of the angle is equal to the side opposite to acute angle divided by the adjacent side of acute angle.
III.Angle of elevation is the upward angle from the horizontal line opf the sight from the observer to to some point of interest