Question

The angle of elevation of a cloud from a point $200$ m above the lake is${30^ \circ }$ and the angle of depression of its reflection to the lake is ${60^ \circ }$. Find the height of the cloud above the lake.

Answer 1

Hint: We will firstly draw the required figure for the question. We will use trigonometric identities for this question, mainly $\tan \theta = \dfrac{P}{B}$,$\theta$ being the angles of elevation and depression accordingly and $P$is the perpendicular and $B$ is the base of the triangle.

Complete step-by-step answer:
According to the question, we know that the angle of elevation is ${30^ \circ }$ and the angle of depression is ${60^ \circ }$. The angle of elevation is measured from a point $200$ m above the surface of the said lake.
Let us now start by drawing the required diagram. Let $BC$ be the surface of the lake. Let $D$ be the point $200$m above the surface of the lake, $\therefore CD = 200$m. Let $O$ be the cloud. $O'$ is the reflection of the cloud on the lake.
The angle of elevation $= \angle ODA = {30^ \circ }$
The angle of depression $= \angle O'DA = {60^ \circ }$

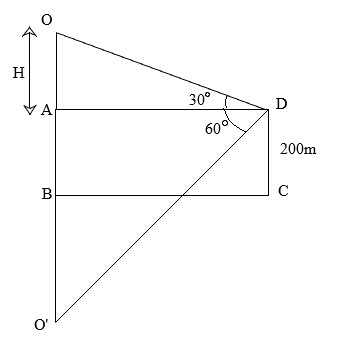
Let $OA = H$,$H$ is the height of the cloud $200$ m above the surface of the lake.

$$\Rightarrow AB = CD = 200m \\\ \Rightarrow O'B = OB = 200 + H \\\$$

According to the properties of reflection, the height of the cloud O above the lake-level is equal to the depth of its image O’ below the lake level, so $O'B = OB$.
Now, in $\Delta OAD,$

$$\tan {30^ \circ } = \dfrac{{OA}}{{AD}} \\\ \Rightarrow \tan {30^ \circ } = \dfrac{H}{{AD}} \\\ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{H}{{AD}} \\\ \Rightarrow AD = \sqrt 3 H \\\$$

In$\Delta O'AD,$

$$\tan {60^ \circ } = \dfrac{{O'A}}{{AD}} \\\ \Rightarrow \tan {60^ \circ } = \dfrac{{O'B + AB}}{{AD}} \\\ \Rightarrow \sqrt 3 = \dfrac{{OB + AB}}{{AD}} \\\ \Rightarrow \sqrt 3 = \dfrac{{200 + H + 200}}{{AD}} \\\ \Rightarrow \sqrt 3 = \dfrac{{400 + H}}{{AD}} \\\ \\\$$

We are using $\tan$ here because the base is common in both the triangles and the perpendicular is known to us.
Now substituting the value of $AD$ in the equation, we get

$$\sqrt 3 = \dfrac{{400 + H}}{{\sqrt 3 H}} \\\ \Rightarrow \sqrt 3 \times \sqrt 3 H = 400 + H \\\ \Rightarrow 3H = 400 + H \\\ \Rightarrow 3H - H = 400 \\\ \Rightarrow 2H = 400 \\\ \Rightarrow H = \dfrac{{400}}{2} \\\ \Rightarrow H = 200 \\\$$

Therefore, the height of the cloud from the surface of the lake $= AB + H = 200 + 200 = 400$ m.

Note: In these types of problems, we always start with making the diagram as required by the question. We need to remember that the angle of elevation is equal to the angle of depression as when we make a diagram representing the line of sight, we see that the horizontal in the angle of depression and the horizontal or base in the angle of elevation are parallel. Thus, applying the properties of parallel lines, we get the angle of elevation to be equal to the angle of depression because they are alternate angles. We are using $\tan$ in these questions because we mainly work with heights and distance from the given object.