Question

The angle of elevation from the top of a rock and the foot to the top of a 60m high tower are ${45^0}{\text{ and 6}}{{\text{0}}^0}$respectively. Find the height of the rock. $\left( {\sqrt 3 = 1.732} \right)$.

Answer 1

Hint: Let the height of the rock to be variable, use the concept of trigonometric ratios to figure out respective triangles through which the value of this variable could be calculated. Use of $\tan \theta$ would be more suitable.

Complete step-by-step answer:

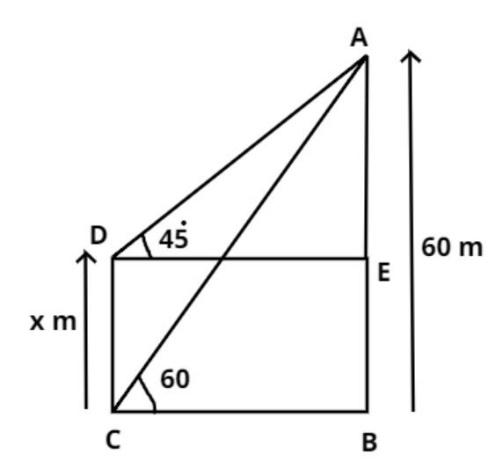
Let DC be the rock and AB be the high tower.
Let the height of the rock be x meter.
Now it is given that the height of the high tower is 60 meter.
Therefore AB = 60 meter.
The angle of elevation of the top of a rock from the top and foot of a 60 meter high tower are 45 and 60 degree respectively (see figure).
$\Rightarrow \angle ADE = {45^0},\angle ACB = {60^0}$
So by symmetry DC = EB = x meter.
So from figure AB = AE + EB
$\Rightarrow 60 = AE + x$
$\Rightarrow AE = 60 - x$ meter.
Now in triangle ADE,
$\Rightarrow \tan {45^0} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} = \dfrac{{AE}}{{DE}} = \dfrac{{60 - x}}{{DE}}$
$\Rightarrow 1 = \dfrac{{60 - x}}{{DE}}$
$\Rightarrow DE = 60 - x$ meter.
So by symmetry (BC = 60 –x) meter.
Now in triangle ABC,
$\Rightarrow \tan {60^0} = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}} = \dfrac{{AB}}{{BC}} = \dfrac{{60}}{{60 - x}}$
Now as we know that the value of $\tan {60^0} = \sqrt 3$ so substitute this value in above equation we have,
$\Rightarrow \sqrt 3 = \dfrac{{60}}{{60 - x}}$
Now simplifying we get,
$\Rightarrow 60\sqrt 3 - x\sqrt 3 = 60$
$\Rightarrow x = \dfrac{{60\sqrt 3 - 60}}{{\sqrt 3 }}$
Now substitute $\sqrt 3 = 1.732$ we have,
$\Rightarrow x = \dfrac{{\left( {60 \times 1.732} \right) - 60}}{{1.732}} = \dfrac{{60 \times 0.732}}{{1.732}} = 25.36$ meter.
So this is the required height of the rock.

Note: Whenever we face such types of problems the key concept is to build a diagrammatic representation through the provided question’s information as it helps in understanding the geometry of the question and thus respective triangles in which trigonometric ratios are to be applied can be figured out quickly.