Question
Question: The angle of deviation when light is incident at an angle of \(45{}^\circ \) on one of the refractin...
The angle of deviation when light is incident at an angle of 45∘ on one of the refracting faces of an equilateral prism of refractive index 1.414 is
A. 40∘B. 30∘C. 45∘D. 50∘
Solution
Hint: By using the formula of refractive index for prism, we get the correct answer. The angle of deviation of a ray of light passing through a prism depends upon its material as well as on the angle of incidence. Here it means it depends upon the refractive index of a material of prism.
Complete answer step by step:
The given prism is equilateral so the three angles are of 60∘. So, ∠A=60∘.
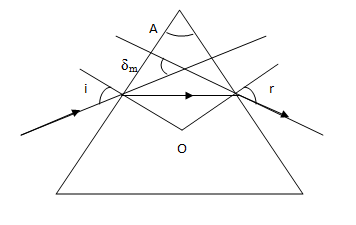
The angle of incident is given,
∠i=45∘
We know that the equation for refractive index of prism,
μ=sin(2A)sin[2A+δm]
where µ is the refractive index of prism and δm is angle of deviation.
Substituting given values in above equation we get,
1.414=sin(260∘)sin[260∘+δm]=sin(30∘)sin[260∘+δm]
We know sin(30∘)=21=0.5, so above equation can be written as,
1.414×0.5=sin[260∘+δm]
0.707=sin[260∘+δm]
Multiplying both sides by sin−1, we get
sin−1(0.707)=[260+δm]
We know, sin(45∘)=21=0.707, so above equation can be written as,
