Question

The angle of deviation of a cloud from a point h meter above a lake is $\theta$. The angle of depression of its reflection in the lake is ${{45}^{\circ }}$. The height of the cloud
(a)$h\tan \left( {{45}^{\circ }}+\theta \right)$
(b)$h\cot \left( {{45}^{\circ }}-\theta \right)$
(c)$h\tan \left( {{45}^{\circ }}-\theta \right)$
(d)$h\cot \left( {{45}^{\circ }}-\theta \right)$

Answer 1

Hint: At first take the angle of depression as $\phi$, then draw the diagram according to the question given. After that apply the trigonometric ratio tan to both the triangles containing $\theta$ and $\phi$ and then compare them. After comparing, put the value of $\phi$ as ${{45}^{\circ }}$ to find what is asked.

Complete step-by-step answer:
At first we will do the question in the generalized form which is let’s suppose the angle of depression be $\phi$. Let’s suppose height of cloud from ground be H. So, we will draw the diagram as,

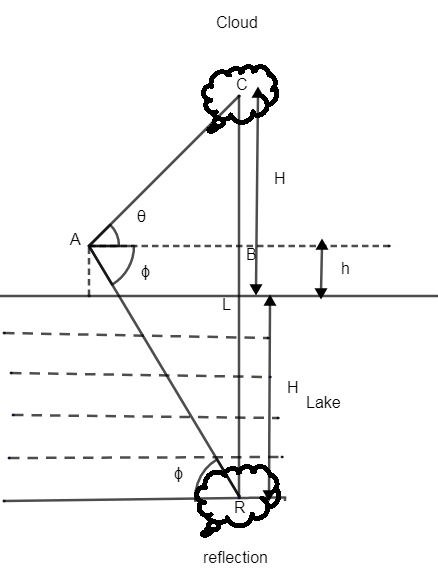
Let A be the point from where observations were taken which is h length from the surface of the lake.
Now let’s consider triangle ABC, here we will apply trigonometric ratio which is
$\tan \theta =$Opposite side of angle $\theta$ / adjacent side of angle $\theta$
Opposite side length which is CB will be calculated as (H - h) and adjacent side will be $\tan \theta$ is equal to $\dfrac{H-h}{AB}$.
So, we can write AB as, $\dfrac{H-h}{\tan \theta }$.
Now let’s consider triangle ABR, here we will apply trigonometric ratio which is,
$\tan \phi =$ Opposite side of angle $\phi$ / adjacent side of angle $\phi$
Opposite side length which is BR will be calculated as (H + h) and the adjacent side will be represented as AB.
So, the value of $\tan \phi$ is equal to $\dfrac{H+h}{AB}$.
So, we can write AB as, $\dfrac{H+h}{\tan \phi }$.
Now we know that the value of AB is $\dfrac{H-h}{\tan \theta }$ and also the value of AB is $\dfrac{H+h}{\tan \phi }$.
So, we can equate and write it as,
$\dfrac{H-h}{\tan \theta }=\dfrac{H+h}{\tan \phi }$
Or, $\dfrac{H-h}{H-h}=\dfrac{\tan \theta }{\tan \phi }$
Now, we will apply componendo and dividendo which means that if,
$\dfrac{a+b}{a-b}=\dfrac{c}{d}$
Then we can write it as,
$\dfrac{a+b+a-b}{a+b-a+b}=\dfrac{c+d}{d-d}$
Or, $\dfrac{2a}{2b}=\dfrac{c+d}{c-d}$
Or, $\dfrac{a}{b}=\dfrac{c+d}{c-d}$
So, on applying componendo and dividendo we get,
$\dfrac{H+h+H-h}{H+h-H+h}=\dfrac{\tan \phi +\tan \theta }{\tan \phi -\tan \theta }$
Or, $\dfrac{2H}{2h}=\dfrac{\tan \phi +\tan \theta }{\tan \phi -\tan \theta }$
Or, $\dfrac{H}{h}=\dfrac{\tan \phi +\tan \theta }{\tan \phi -\tan \theta }$
So, $H=h\left( \dfrac{\tan \phi +\tan \theta }{\tan \phi -\tan \theta } \right)$
As we took it in the generalized form we got value of H like this now as we know value of $\tan \phi$ is $\tan {{45}^{\circ }}$ as $\phi ={{45}^{\circ }}$. So, the value of H will be,
$H=h\left( \dfrac{1+\tan \theta }{1-\tan \theta } \right)$
We know the formula that,
$\tan \left( x+y \right)=\dfrac{\tan x+\tan y}{1-\tan x\tan y}$
So, we can put x as ${{45}^{\circ }}$ and y as $\theta$.
So, $\tan \left( 45+\theta \right)=\dfrac{\tan {{45}^{\circ }}+\tan \theta }{1-\tan {{45}^{\circ }}\tan \theta }$
Or, $\tan \left( 45+\theta \right)=\dfrac{1+\tan \theta }{1-\tan \theta }$
So, we can write $\dfrac{1+\tan \theta }{1-\tan \theta }$ as $\tan \left( 45+\theta \right)$.
Hence, H is equal to $h\tan \left( {{45}^{\circ }}+\theta \right)$.
So, the correct option is (a).

Note: While doing calculations, one should be very careful as any small mistake can result in a wrong answer. Also, the trigonometric ratios of standard angles should be remembered as they are used very often in such questions.