Question

The angle of depression of two ships from an aeroplane flying at the height of 7500m are ${30^ \circ }$ and ${45^ \circ }$ . If both the ships are in the same line and one ship is exactly behind the other, find the distance between the ships.

Answer 1

We will first sketch the situation and then using trigonometric formula of $\tan \theta = \dfrac{{perpendicular}}{{base}}$, we will calculate the distance between the ships.

_Complete step-by-step answer: _
We are given that an aeroplane is flying at a height of 7500m from the sea level and the angle of depression of two ships from the aeroplane are ${30^ \circ }$ and ${45^ \circ }$. Then, the figure of this condition will be:

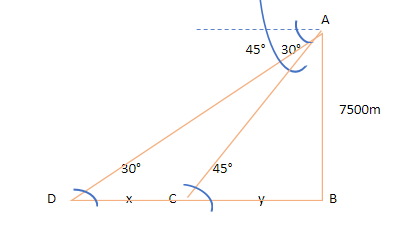
Consider the figure given above, from it we can say that $\angle ADB = {30^ \circ } \\\ \angle ACB = {45^ \circ } \\\$ . It is so because of the property that alternate angles between two parallel lines are equal.
Let DC, the distance between the ships, be x and CB be y (which is the distance of the the first ship from the foot of the perpendicular drawn from the aeroplane)
$\therefore$ DB= x + y
Now in $\vartriangle ABC$, $\tan {45^ \circ } = \dfrac{{AB}}{{BC}} = \dfrac{{7500}}{y}$
$\Rightarrow 1 = \dfrac{{7500}}{y} \\\ \Rightarrow y = 7500 \\\$
Similarly, in the $\vartriangle ABD$, $\tan {30^ \circ } = \dfrac{{AB}}{{BD}} = \dfrac{{7500}}{{x + y}}$
$\Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{7500}}{{x + y}} \\\ \Rightarrow x + y = 7500\sqrt 3 \\\ \Rightarrow x + 7500 = 7500\sqrt 3 \\\ \Rightarrow x = 7500(\sqrt 3 - 1) \\\ \Rightarrow x = 7500\left( {1.73 - 1} \right) \\\ \Rightarrow x = 7500 \times 0.73 \\\ \Rightarrow x = 5475m \\\$ (we know that $\sqrt 3 = 1.73$)
Hence, the distance between the two ships is 5475m.

Note: In such problems where the angle of depression is given, students might get confused by how to solve it further. So, you need to draw a figure first hand and then you can have a clear idea about what is asked from the question. Converting the angle of depression into an angle of elevation will be helpful in calculating the tangent of the angles.