Question

The angle between two vectors $A$ and $B$ is $\theta$ .Vector $R$ is the resultant of the two vectors. If $R$ makes an angle $\dfrac{\theta }{2}$ with $A$, then

A.)$A = 2B$
B.)$A = \dfrac{B}{2}$
C.)$A = B$
D.$AB = 1$

Answer 1

Hint – You can start the solution by drawing a well-labelled diagram with all the vectors ($A$,$B$and$R$) originating from a common point. The equations for the magnitude of the resultant vector and the direction of the resultant vector are $R = \sqrt {{A^2} + {B^2} + 2AB\operatorname{Cos} \theta }$ and $\tan \alpha = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$ respectively. Use the second equation given above to reach the solution.

Complete answer:
To solve this equation, consider the diagram given below

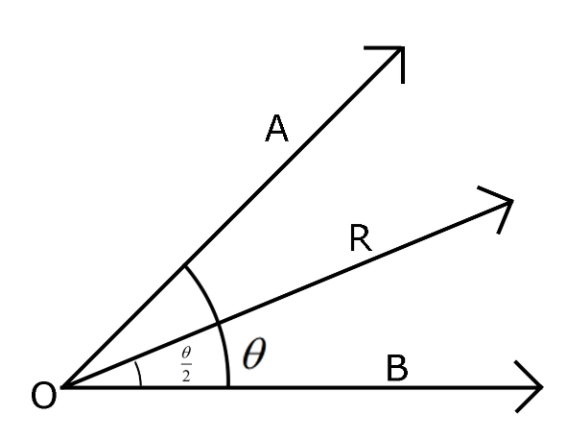
The arrangement of $A$, $B$ and $R$ (Resultant) vectors is done in such a way that it is easy to co-relate with the other two vectors.
We know,

$\angle AOB = \theta$,
And $\angle ROA = \dfrac{\theta }{2}$

We also know,

$\angle BOR = \angle AOB - \angle ROA$
$\Rightarrow \angle BOR = \theta - \dfrac{\theta }{2}$
$\Rightarrow \angle BOR = \dfrac{\theta }{2}$

The equation for the $\angle ROA$ is as follows –

$\tan \alpha = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$
$\Rightarrow \dfrac{{\sin (\dfrac{\theta }{2})}}{{\cos (\dfrac{\theta }{2})}} = \dfrac{{2B(\dfrac{\theta }{2})\cos (\dfrac{\theta }{2})}}{{A + B\cos \theta }}$
$\Rightarrow A + B\cos \theta = B{\cos ^2}\theta (\dfrac{\theta }{2})$
$\Rightarrow A + B[2{\cos ^2}(\dfrac{\theta }{2}) - 1] = 2B{\cos ^2}(\dfrac{\theta }{2})$
$\Rightarrow A = B$

Hence, Option C is the correct option

Additional Information:
A vector is a mathematical quantity that has both a magnitude (size) and a direction. To imagine what a vector is like, imagine asking someone for directions in an unknown area and they tell you, “Go $5km$ towards the West”. In this sentence, we see an example of a displacement vector, “$5km$” is the magnitude of the displacement vector and “towards the North” is the indicator of the direction of the displacement vector.
A vector quantity is different from a scalar quantity in the fact that a scalar quantity has only magnitude, but a vector quantity possesses both direction and magnitude. Unlike scalar quantities, vector quantities cannot undergo any mathematical operation, instead they undergo Dot product and Cross product.
Some examples of vectors are – Displacement, Force, Acceleration, Velocity, Momentum, etc.

Note – You can also get to the solution by not going through the mathematical calculations and just focusing on the theoretical part. You can make an argument that we know that $\angle BOR = \dfrac{\theta }{2}$ as , and. If the angles of the vector are the same with bothand. Then we can safely conclude that $A = B$, as only this condition can satisfy the given data.