Solveeit Logo
Login

Question

Question: The angle between two perpendicular lines is: a) \({{90}^{\circ }}\) b) \({{60}^{\circ }}\) ...

The angle between two perpendicular lines is:
a) 90∘{{90}^{\circ }}
b) 60∘{{60}^{\circ }}
c) 45∘{{45}^{\circ }}
d) 120∘{{120}^{\circ }}

Explanation

Solution

Hint : In this question, we are given that the lines are perpendicular. Therefore, we can form the two angles made by the two lines at the point of intersection. We can then use the fact the sum of two angles in which two sides are part of a common straight line is equal to180∘{{180}^{\circ }} . As the two lines are perpendicular the two formed angles should be equal and their sum should be equal to 180∘{{180}^{\circ }} . Therefore, each of these angles should be equal to 90∘{{90}^{\circ }} .

Complete step by step solution :
Let the two perpendicular lines intersect at the point O. Let A be a point on the first line and B and C be points on the second line as shown in the figure.

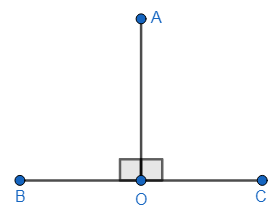
We know that fact the sum of two angles in which two sides are part of a common straight line is equal to180∘{{180}^{\circ }}. Therefore, we can write
∠AOB+∠AOC=180∘.......................(1.1)\angle AOB+\angle AOC={{180}^{\circ }}.......................(1.1)
Also, as the lines are given to be perpendicular both the formed angles should be equal, therefore, we should have
∠AOB=∠AOC......................(1.2)\angle AOB=\angle AOC......................(1.2)
Therefore, using equation (1.2) in (1.1), we obtain
∠AOB+∠AOB=180∘ ⇒2∠AOB=180∘ ⇒∠AOB=180∘2=90∘ \begin{aligned} & \angle AOB+\angle AOB={{180}^{\circ }} \\\ & \Rightarrow 2\angle AOB={{180}^{\circ }} \\\ & \Rightarrow \angle AOB=\dfrac{{{180}^{\circ }}}{2}={{90}^{\circ }} \\\ \end{aligned}
Therefore, using this in equation (1.2), we obtain ∠AOB=∠AOC=90∘\angle AOB=\angle AOC={{90}^{\circ }} .
Thus, the angle between two perpendicular lines is 90∘{{90}^{\circ }} which matches option (a). Therefore, option (a) is the correct answer to this question.

Note : We should note that as both the formed angles are equal we should not get confused about which of the two formed angles we should consider as both of them have the same angle and thus will give the same answer.