Question

The angle between the tangents drawn to ${{(y-2)}^{2}}=4(x+3)$ at the point where it is intersected by the line $3x-y+8=0$ is $\dfrac{4\pi }{p}$ , then $p$ has the value equal to
(a) 13
(b) 8
(c) $10\sqrt{5}$
(d) 4

Answer 1

Find the intersection point of parabola ${{(y-2)}^{2}}=4(x+3)$ and line $3x-y+8=0$ . Find the derivative of ${{(y-2)}^{2}}=4(x+3)$ with respect to x which will be the slope of line of tangent using the point of intersection. Use the formula for angles between two slopes ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ to find the value of angle $\theta$ .

Complete step by step answer:
In the question it is given that ${{(y-2)}^{2}}=4(x+3).........(1)$ is an equation of parabola and $3x-y+8=0$ is an equation of straight line.

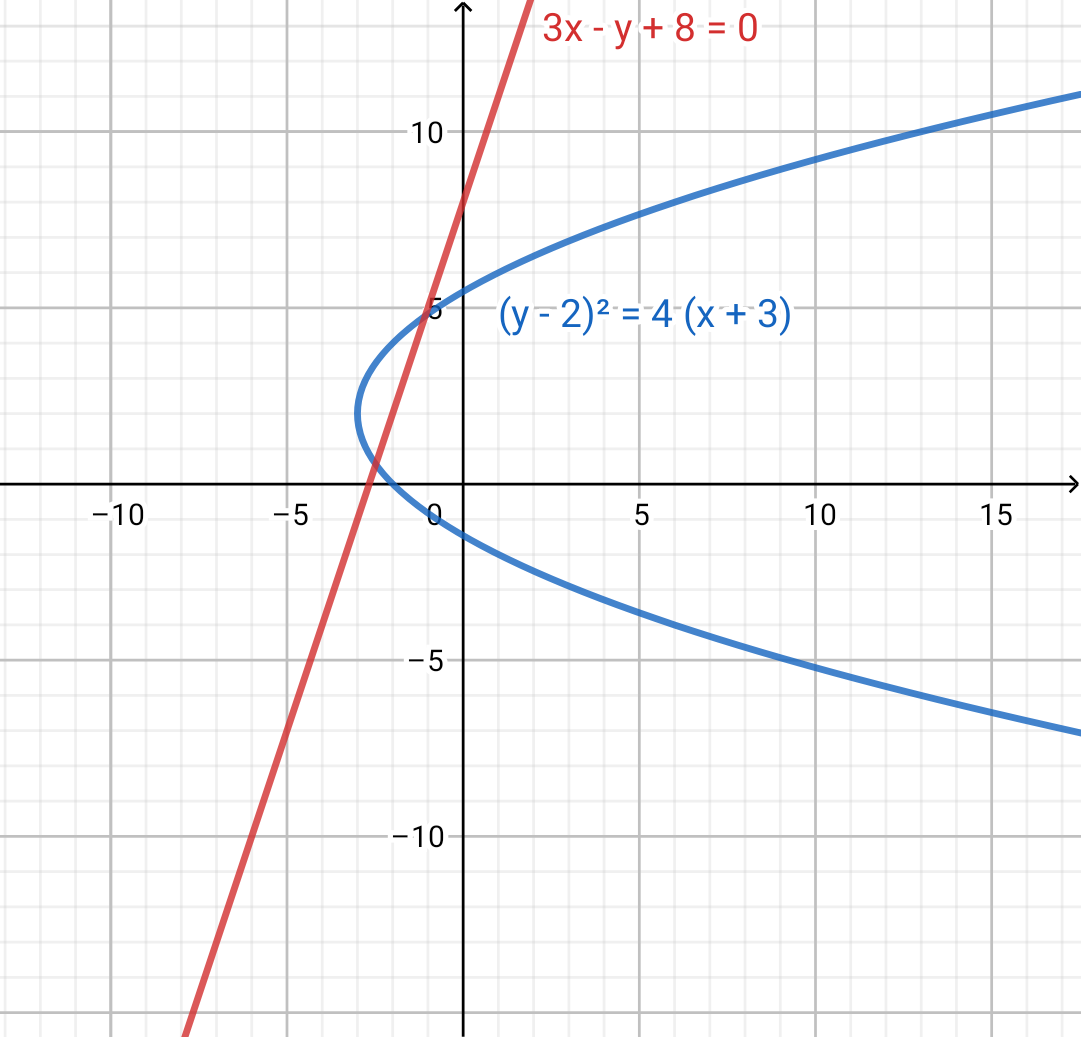
We have to find the angles between the tangents drawn to ${{(y-2)}^{2}}=4(x+3)$ at the point where it is intersected by the line $3x-y+8=0$. So first we will find the point of intersection between these two curves. $3x-y+8=0$ can be written as $y=3x+8$ . We will now substitute the value of $y$ in equation (1) we get,
${{(3x+8-2)}^{2}}=4(x+3)$
${{(3x+6)}^{2}}=4(x+3)$
Now we simplify the equation by squaring the terms on the left side of the equation and on the right hand side multiply 4 to the bracket.
$9{{x}^{2}}+36+36x=4x+12$
Combine the like terms and then simplify it.
$9{{x}^{2}}+(36-12)+(36x-4x)=0$
$9{{x}^{2}}+32x+24=0........(2)$
We will find the roots of the above equation by using the formula $x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$ where $a{{x}^{2}}+bx+c=0$ is the given quadratic equation. Here a=9, b=32 and c=24 so the roots of equation (2) is
$x=\dfrac{-32\pm \sqrt{{{32}^{2}}-4(9)(24)}}{2(9)}$
$x=\dfrac{-32\pm \sqrt{1024-864}}{18}$
The value of $\sqrt{1024-864}$ is $\sqrt{160}$ . And the value of $\sqrt{160}$ is $4\sqrt{10}$ .
$x=\dfrac{-32\pm \sqrt{160}}{18}$
$x=\dfrac{-32\pm 4\sqrt{10}}{18}$
Multiplying numerator and denominator by 2 the above equation becomes
$x=\dfrac{-16\pm 2\sqrt{10}}{9}$
The two roots of equation (2) is ${{x}_{1}}=\dfrac{-16+2\sqrt{10}}{9}$ and ${{x}_{2}}=\dfrac{-16-2\sqrt{10}}{9}$ . For finding the value of y we will substitute the value of ${{x}_{1}}$ and ${{x}_{2}}$ in $y=3x+8$ we will get two values of y that is ${{y}_{1}}=\dfrac{8+2\sqrt{10}}{3}$ and ${{y}_{2}}=\dfrac{8-2\sqrt{10}}{3}$ . Now we will differentiate the equation of parabola ${{(y-2)}^{2}}=4(x+3)$ with respect to $x$ .
After differentiating we get,
$2(y-2)\dfrac{dy}{dx}=4$
$\dfrac{dy}{dx}=\dfrac{2}{(y-2)}.......(3)$
The above derivative represents the slope. Substituting $y={{y}_{1}}$ and $y={{y}_{2}}$ we get two slopes ${{m}_{1}}=\dfrac{2}{({{y}_{1}}-2)}$ and ${{m}_{2}}=\dfrac{2}{({{y}_{2}}-2)}$ . We know that angle between two lines having slope ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ . Substitute the values of ${{m}_{1}}$ and ${{m}_{2}}$ to find the angle between slopes. We get
$\tan \theta =\left| \dfrac{\left( \dfrac{2}{{{y}_{2}}-2} \right)-\left( \dfrac{2}{{{y}_{1}}-2} \right)}{1+\left[ \dfrac{2}{{{y}_{2}}-2} \right]\left[ \dfrac{2}{{{y}_{1}}-2} \right]} \right|$
Solve the above equation by first simplifying the numerator and then the denominator, After simplifying we get.
$\tan \theta =\left| \dfrac{2({{y}_{1}}-2)-2({{y}_{2}}-2)}{({{y}_{2}}-2)({{y}_{1}}-2)+4} \right|$
$\tan \theta =\left| \dfrac{2{{y}_{1}}-4-2{{y}_{2}}+4)}{{{y}_{1}}{{y}_{2}}-2{{y}_{2}}-2{{y}_{1}}+4+4} \right|$
In the numerator adding -4 and 4 becomes 0 and in denominator adding 4 and 4 we get 8 so the above equation becomes,
$\tan \theta =\left| \dfrac{2{{y}_{1}}-2{{y}_{2}})}{{{y}_{1}}{{y}_{2}}-2{{y}_{2}}-2{{y}_{1}}+8} \right|$
Now substitute the values of ${{y}_{1}}$ and ${{y}_{2}}$ which we have found earlier in the above equation.
$\tan \theta =\left| \dfrac{2\left( \dfrac{8+2\sqrt{10}}{3} \right)-2\left( \dfrac{8-2\sqrt{10}}{3} \right)}{\left( \dfrac{8-2\sqrt{10}}{3} \right)\left( \dfrac{8+2\sqrt{10}}{3} \right)-2\left( \dfrac{8-2\sqrt{10}}{3} \right)-2\left( \dfrac{8+2\sqrt{10}}{3} \right)+8} \right|$
Solving the numerator and denominator part we get,
$\tan \theta =\left| \dfrac{\left( \dfrac{16+4\sqrt{10}-16+4\sqrt{10}}{3} \right)}{\left( \dfrac{24}{9} \right)-\left( \dfrac{16-4\sqrt{10}+16+4\sqrt{10}}{3} \right)+8} \right|$
Solving $\left( \dfrac{16+4\sqrt{10}-16+4\sqrt{10}}{3} \right)$ we get $\left( \dfrac{8\sqrt{10}}{3} \right)$ and solving $\left( \dfrac{16-4\sqrt{10}+16+4\sqrt{10}}{3} \right)$ we get $\left( \dfrac{32}{3} \right)$ . The above equation now becomes,
$\tan \theta =\left| \dfrac{\left( \dfrac{8\sqrt{10}}{3} \right)}{\left( \dfrac{8}{3} \right)-\left( \dfrac{32}{3} \right)+8} \right|$
$\tan \theta =\left| \dfrac{\left( \dfrac{8\sqrt{10}}{3} \right)}{\left( \dfrac{8-32+24}{3} \right)} \right|$
After adding 8-32+24 we get 0 as answer so the denominator becomes 0 then the value of $\tan \theta$ becomes
$\tan \theta =\left| \dfrac{\left( \dfrac{8\sqrt{10}}{3} \right)}{(0)} \right|$
$\tan \theta =\infty$
Since $\tan \theta =\infty$ the value of $\theta$ is $\dfrac{\pi }{2}$ . And in the question it is given that the angle is equal to $\dfrac{4\pi }{p}$ , we have to find the value of $p$ so we will equate both the values of angle to find the value of $p$ ,
$\dfrac{4\pi }{p}=\dfrac{\pi }{2}$
$p=8$
Hence the value of $p=8$ .

Note:
Angle between two lines having slope ${{m}_{1}}$ and ${{m}_{2}}$ is given by $\tan \theta =\left| \dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ . Substitute the values of ${{m}_{1}}$ and ${{m}_{2}}$ to find the angle between slopes. Where ${{m}_{1}}=\dfrac{2}{({{y}_{1}}-2)}$ and ${{m}_{2}}=\dfrac{2}{({{y}_{2}}-2)}$ . Then $\tan \theta =\left| \dfrac{\left( \dfrac{2}{{{y}_{2}}-2} \right)-\left( \dfrac{2}{{{y}_{1}}-2} \right)}{1+\left[ \dfrac{2}{{{y}_{2}}-2} \right]\left[ \dfrac{2}{{{y}_{1}}-2} \right]} \right|$ . Care should be taken while calculating this expression, plus and minus sign should not be interchanged.