Question
Question: The angle between the tangents drawn to \({{(y-2)}^{2}}=4(x+3)\) at the point where it is intersecte...
The angle between the tangents drawn to (y−2)2=4(x+3) at the point where it is intersected by the line 3x−y+8=0 is p4π , then p has the value equal to
(a) 13
(b) 8
(c) 105
(d) 4
Solution
Find the intersection point of parabola (y−2)2=4(x+3) and line 3x−y+8=0 . Find the derivative of (y−2)2=4(x+3) with respect to x which will be the slope of line of tangent using the point of intersection. Use the formula for angles between two slopes m1 and m2 is given by tanθ=1+m1m2m2−m1 to find the value of angle θ .
Complete step by step answer:
In the question it is given that (y−2)2=4(x+3).........(1) is an equation of parabola and 3x−y+8=0 is an equation of straight line.
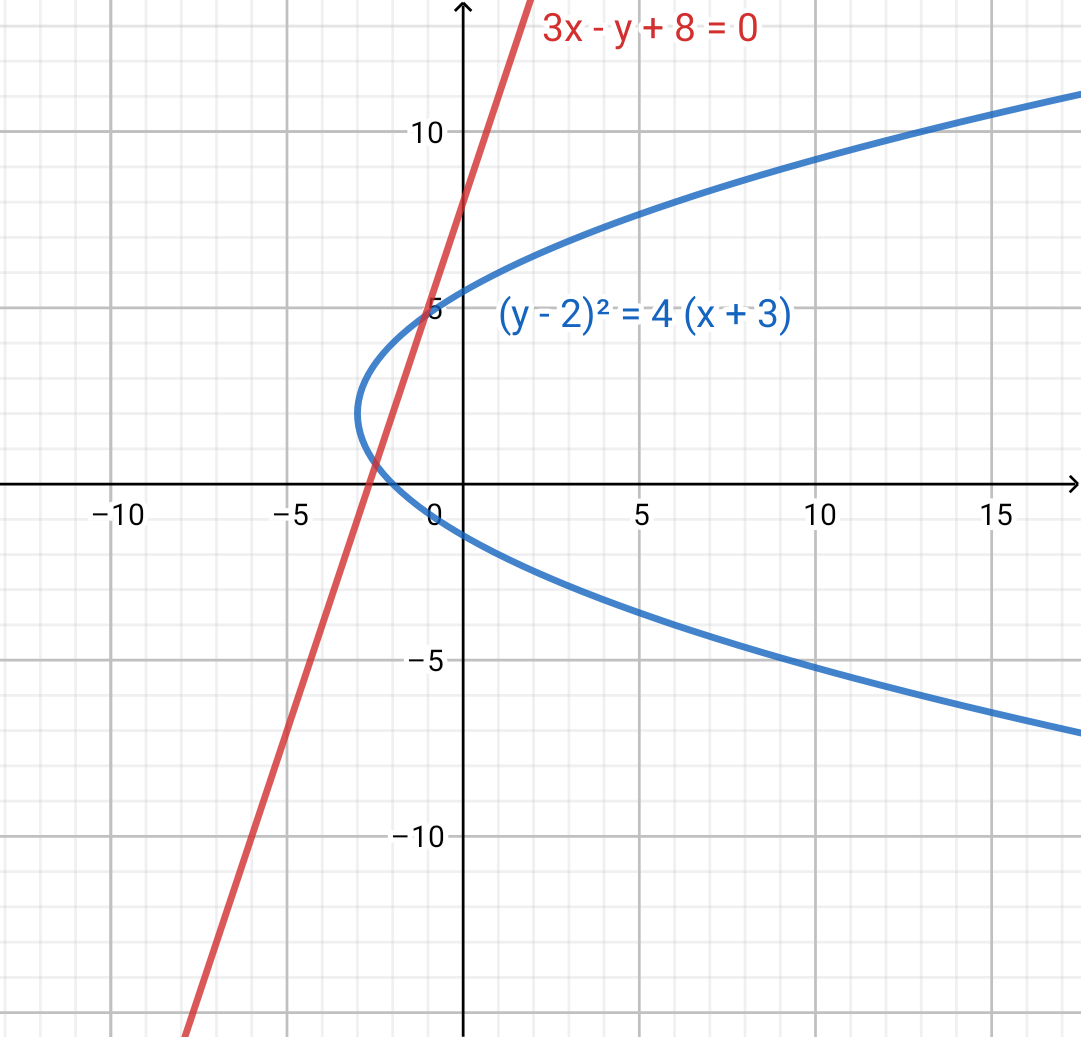
We have to find the angles between the tangents drawn to (y−2)2=4(x+3) at the point where it is intersected by the line 3x−y+8=0. So first we will find the point of intersection between these two curves. 3x−y+8=0 can be written as y=3x+8 . We will now substitute the value of y in equation (1) we get,
(3x+8−2)2=4(x+3)
(3x+6)2=4(x+3)
Now we simplify the equation by squaring the terms on the left side of the equation and on the right hand side multiply 4 to the bracket.
9x2+36+36x=4x+12
Combine the like terms and then simplify it.
9x2+(36−12)+(36x−4x)=0
9x2+32x+24=0........(2)
We will find the roots of the above equation by using the formula x=2a−b±b2−4ac where ax2+bx+c=0 is the given quadratic equation. Here a=9, b=32 and c=24 so the roots of equation (2) is
x=2(9)−32±322−4(9)(24)
x=18−32±1024−864
The value of 1024−864 is 160 . And the value of 160 is 410 .
x=18−32±160
x=18−32±410
Multiplying numerator and denominator by 2 the above equation becomes
x=9−16±210
The two roots of equation (2) is x1=9−16+210 and x2=9−16−210 . For finding the value of y we will substitute the value of x1 and x2 in y=3x+8 we will get two values of y that is y1=38+210 and y2=38−210 . Now we will differentiate the equation of parabola (y−2)2=4(x+3) with respect to x .
After differentiating we get,
2(y−2)dxdy=4
dxdy=(y−2)2.......(3)
The above derivative represents the slope. Substituting y=y1 and y=y2 we get two slopes m1=(y1−2)2 and m2=(y2−2)2 . We know that angle between two lines having slope m1 and m2 is given by tanθ=1+m1m2m2−m1 . Substitute the values of m1 and m2 to find the angle between slopes. We get
tanθ=1+[y2−22][y1−22](y2−22)−(y1−22)
Solve the above equation by first simplifying the numerator and then the denominator, After simplifying we get.
tanθ=(y2−2)(y1−2)+42(y1−2)−2(y2−2)
tanθ=y1y2−2y2−2y1+4+42y1−4−2y2+4)
In the numerator adding -4 and 4 becomes 0 and in denominator adding 4 and 4 we get 8 so the above equation becomes,
tanθ=y1y2−2y2−2y1+82y1−2y2)
Now substitute the values of y1 and y2 which we have found earlier in the above equation.
tanθ=(38−210)(38+210)−2(38−210)−2(38+210)+82(38+210)−2(38−210)
Solving the numerator and denominator part we get,
tanθ=(924)−(316−410+16+410)+8(316+410−16+410)
Solving (316+410−16+410) we get (3810) and solving (316−410+16+410) we get (332) . The above equation now becomes,
tanθ=(38)−(332)+8(3810)
tanθ=(38−32+24)(3810)
After adding 8-32+24 we get 0 as answer so the denominator becomes 0 then the value of tanθ becomes
tanθ=(0)(3810)
tanθ=∞
Since tanθ=∞ the value of θ is 2π . And in the question it is given that the angle is equal to p4π , we have to find the value of p so we will equate both the values of angle to find the value of p ,
p4π=2π
p=8
Hence the value of p=8 .
Note:
Angle between two lines having slope m1 and m2 is given by tanθ=1+m1m2m2−m1 . Substitute the values of m1 and m2 to find the angle between slopes. Where m1=(y1−2)2 and m2=(y2−2)2 . Then tanθ=1+[y2−22][y1−22](y2−22)−(y1−22) . Care should be taken while calculating this expression, plus and minus sign should not be interchanged.
