Question

The angle between the pair of straight lines $x^2 + 4y^2 - 7xy = 0$, is

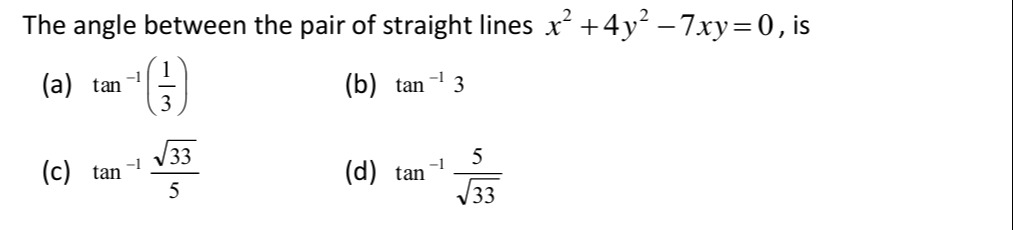
• A. $tan^{-1}(\frac{1}{3})$
• B. $tan^{-1}3$
• C. $tan^{-1}\frac{\sqrt{33}}{5}$
• D. $tan^{-1}\frac{5}{\sqrt{33}}$

Answer 1

Answer: (C)

$tan^{-1}\frac{\sqrt{33}}{5}$

Answer 2

The given equation of the pair of straight lines is $x^2 - 7xy + 4y^2 = 0$. This equation is in the form $ax^2 + 2hxy + by^2 = 0$. Comparing the coefficients, we have:

$a = 1$

$2h = -7 \implies h = -\frac{7}{2}$

$b = 4$

The angle $\theta$ between the pair of straight lines represented by $ax^2 + 2hxy + by^2 = 0$ is given by the formula:

$\tan \theta = \left| \frac{2\sqrt{h^2 - ab}}{a + b} \right|$

First, calculate $h^2 - ab$:

$h^2 = \left(-\frac{7}{2}\right)^2 = \frac{49}{4}$

$ab = (1)(4) = 4$

$h^2 - ab = \frac{49}{4} - 4 = \frac{49 - 16}{4} = \frac{33}{4}$

Next, calculate $a + b$:

$a + b = 1 + 4 = 5$

Substitute these values into the formula for $\tan \theta$:

$\tan \theta = \left| \frac{2\sqrt{\frac{33}{4}}}{5} \right|$

$\tan \theta = \left| \frac{2 \cdot \frac{\sqrt{33}}{\sqrt{4}}}{5} \right|$

$\tan \theta = \left| \frac{2 \cdot \frac{\sqrt{33}}{2}}{5} \right|$

$\tan \theta = \left| \frac{\sqrt{33}}{5} \right|$

Since $\sqrt{33}$ and 5 are positive, the absolute value is $\frac{\sqrt{33}}{5}$.

$\tan \theta = \frac{\sqrt{33}}{5}$

Therefore, the angle $\theta$ is $\tan^{-1}\left(\frac{\sqrt{33}}{5}\right)$.