Question

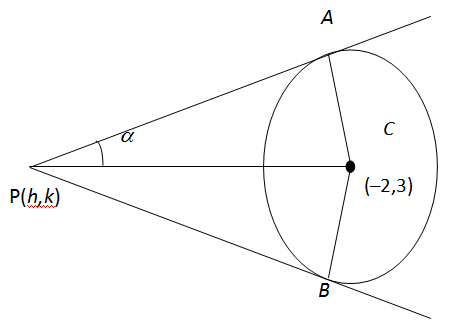
The angle between a pair of tangents drawn from a point P to the circle $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y + 9 \sin ^ { 2 } \alpha + 13 \cos ^ { 2 } \alpha = 0$ is $2 \alpha$ The equation of the locus of the point P is

• A. $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y + 4 = 0$
• B. $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y - 9 = 0$
• C. $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y - 4 = 0$
• D. $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y + 9 = 0$

Answer 1

Answer: (D)

$x ^ { 2 } + y ^ { 2 } + 4 x - 6 y + 9 = 0$

Answer 2

The centre of the circle

$C ( - 2,3 )$ and its radius is $\sqrt { 2 ^ { 2 } + ( - 3 ) ^ { 2 } - 9 \sin ^ { 2 } \alpha - 13 \cos ^ { 2 } \alpha }$

$= \sqrt { 4 + 9 - 9 \sin ^ { 2 } \alpha - 13 \cos ^ { 2 } \alpha } = 2 \sin \alpha$

Let P (h, k) be any point on the locus. The $\angle P A C = \pi / 2$ i.e. triangle APC is a right angle triangle.

Thus $\sin \alpha = \frac { A C } { P C } = \frac { 2 \sin \alpha } { \sqrt { ( h + 2 ) ^ { 2 } + ( k - 3 ) ^ { 2 } } }$

$h ^ { 2 } + k ^ { 2 } + 4 h - 6 k + 9 = 0$Thus the required equation of the locus is $x ^ { 2 } + y ^ { 2 } + 4 x - 6 y + 9 = 0$