Question

The ammeter shown in the figure consists of a $480\Omega$ coil connected in parallel to a $20\Omega$ shunt. The ammeter is then connected to a $140.8\Omega$ resistance and a 20V battery. The reading of ammeter is

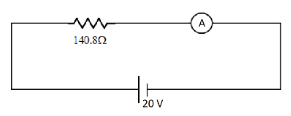
(A) $0.125A$
(B) $1.67A$
(C) $0.13A$
(D) $0.67A$

Answer 1

We are given that two resistances are places in parallel where the $20\Omega$ resistance is a shunt. So then we can calculate the total resistance in the circuit connected with the ammeter and the equivalent resistance will be that in series with $140.8\Omega$ . Now since the emf of the battery is given $20V$ , using that we can find the total current in the circuit having the equivalent resistance. This total current is the reading shown by the ammeter.

Formula used: In this question, we will be using the following formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in series.
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$ where ${R_{eq}}$ is the equivalent resistance when the resistances are placed in a parallel circuit and, $I = \dfrac{V}{R}$ where $I$ is the current in the circuit and $V$ is the emf of the call placed in the circuit.

Complete step by step solution:
We are given that the ammeter given in the figure consists of a coil and a shunt resistance. So the ammeter looks like this,

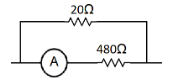
So the resistances $20\Omega$ and $480\Omega$ connected across the ammeter are in parallel, so the total resistance can be found out from the formula,
$\dfrac{1}{{{R_{eq}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ....$
Now here we can put, ${R_1} = 20\Omega$ and ${R_2} = 480\Omega$ . Therefore we get,
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{1}{{20}} + \dfrac{1}{{480}}$
Now taking LCM in the denominator, we get
$\dfrac{1}{{{R_{eq1}}}} = \dfrac{{24 + 1}}{{480}}$
So by taking the reciprocal we get,
${R_{eq1}} = \dfrac{{480}}{{25}}$
The equivalent resistance is, ${R_{eq1}} = 19.2\Omega$
Therefore in the complete circuit, the resistance $140.8\Omega$ is placed in series with the equivalent resistance across the ammeter.
so, to find the equivalent resistance we use the formula,
${R_{eq}} = {R_1} + {R_2} + {R_3} + ....$
Where the values ${R_1} = 140.8\Omega$ and ${R_2} = 19.2\Omega$
Therefore we get the equivalent resistance as,
${R_{eq}} = 140.8 + 19.2$
Adding we get the resistance,
${R_{eq}} = 160\Omega$
Now in the given circuit, the emf of the cell is provided as, $20V$ . So the current in the circuit can be found out from the Ohm’s law as,
$I = \dfrac{V}{R}$
Substituting the values we get,
$I = \dfrac{{20}}{{160}}A$
By doing the division we get,
$I = 0.125A$
Therefore, the reading given by the ammeter will be, $0.125A$
Therefore, the correct option is option (A) $0.125A$.

Note:
The shunt resistance in the question that is connected in parallel to the ammeter is a low resistance path that is provided to the. It is always connected in parallel to the ammeter and sometimes it is built inside the instrument while the other times it is connected externally outside the circuit.