Question

The altitude of the sun when the length of the shadow is $7\sqrt{3}$​m.
A. ${{30}^{o}}$
B. ${{45}^{o}}$
C. ${{60}^{o}}$
D. ${{75}^{o}}$

Answer 1

Hint : Trigonometric functions are real functions in mathematics that relate an angle of a right-angled triangle to ratios of two side lengths. To find a solution to this question, firstly we have to assume the ratio of pole height and shadow length. After that, we need to apply the tangent formula to find the altitude of the sun.

Complete step-by-step answer :
According to question we have the given figure

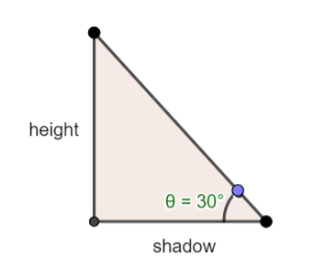
The sun is at a degree of ${{30}^{o}}$
And it is assumed that the length of the pole's shadow is 21m.
Hence,
${{30}^{o}}$ = $\dfrac{pole\text{ }height}{\text{shadow lenght}}$

$$\dfrac{1}{\sqrt{3}}=\dfrac{h}{21} \\\ h=\dfrac{7\times 3}{\sqrt{3}} \\\ h=7\sqrt{3} \\\$$

Now, the altitude of the sun changes; however, the height of the pole remains constant.
It is given that the length of shadow is equal to $7\sqrt{3}$
Let θ be the altitude.
Then, tanθ = $\dfrac{pole\text{ }height}{\text{shadow lenght}}$
tanθ= $\dfrac{7\sqrt{3}}{ 7\sqrt{3}}$
$\tan (\theta )={{45}^{o}}$ = $1$
so, θ= ${{45}^{o}}$
Thus, the answer is option B: 45
So, the correct answer is “Option B”.

Note : The tangent ratio is a branch of trigonometry, which is the branch of mathematics concerned with the relationship between a triangle's sides and angles. Theta is a common variable when working with angles, but other variables can be used as well. When we say opposite, we're referring to the side that's opposite the angle theta. When we say "adjacent," we mean the side that does not form angle theta and is not the hypotenuse. The tangent ratio is the value obtained when the length of the side opposite of angle theta is divided by the length of the side adjacent to angle theta. It is very commonly abbreviated as tan.