Question

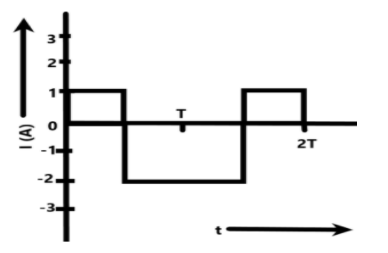
The alternating current in a circuit is described by the graph as shown in the figure. The RMS current obtained from the graph would be –

A) 1.4 A
B) 2.2 A
C) 1.6 A
D) 2.6 A

Answer 1

We need to understand the relation between the current value in an alternating current circuit and its equivalent root mean squared value to solve the problem given to us. The graph has to be interpreted in order to find the RMS value of current.

Complete step by step solution:
The current value in an alternating current circuit varies with time. We know that the current is a sinusoidal function of time. The root mean squared of the current is the equivalent current in a direct current circuit. It is given as –
${{i}_{rms}}=\sqrt{{{i}_{m}}^{2}}$
In the present situation, we are given a time varying current from an alternating current circuit. We can see from the graph below that the current is not changing on a steady basis.

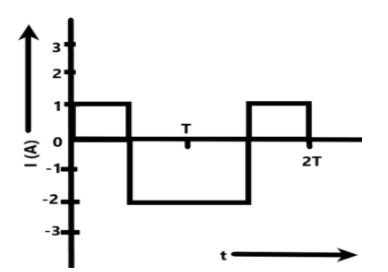
We are given the current details of two complete cycles of the alternating current. We can understand this as the time axis consists of the time ‘2T’ which denotes two time periods. Now, we need to find the RMS value of current for each maximum value of current in the fraction of time period. This is because the current is varying throughout the time.
We can find the RMS value using the relation –
${{i}_{rms}}=\sqrt{\dfrac{{{i}_{1}}^{2}\times {{T}_{1}}+{{i}_{2}}^{2}\times {{T}_{2}}+{{i}_{3}}^{2}\times {{T}_{3}}}{{{T}_{total}}}}$
We can substitute the current values and the time intervals to find the root mean squared value of the current for the given alternating current circuit as –

& {{i}_{rms}}=\sqrt{\dfrac{{{i}_{1}}^{2}\times {{T}_{1}}+{{i}_{2}}^{2}\times {{T}_{2}}+{{i}_{3}}^{2}\times {{T}_{3}}}{{{T}_{total}}}} \\\ & \Rightarrow {{i}_{rms}}=\sqrt{\dfrac{{{1}^{2}}(\dfrac{T}{2})+{{(-2)}^{2}}(T)+{{1}^{2}}(\dfrac{T}{2})}{2T}} \\\ & \Rightarrow {{i}_{rms}}=\sqrt{\dfrac{\dfrac{T}{2}+4T+\dfrac{T}{2}}{2T}} \\\ & \Rightarrow {{i}_{rms}}=\sqrt{\dfrac{5T}{2T}} \\\ & \therefore {{i}_{rms}}=1.58A \\\ \end{aligned}$$ The RMS value of current is almost 1.6 A. **The correct answer is option C.** **Note:** The root mean squared value of current is widely used to understand the quantity of current that will be constant in the alternating circuit. It gives the idea on the current that will be shown by the circuit if it were converted to direct current anytime.