Question

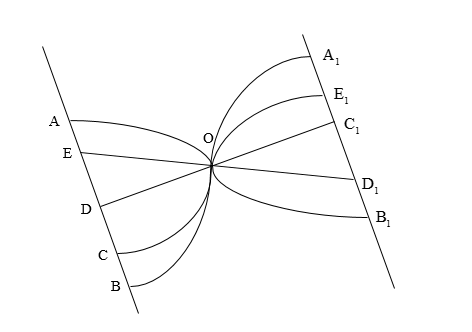
The adjoining figure shows the road plan of lines connecting two parallel roads AB and ${{\rm{A}}_1}{{\rm{B}}_1}$. A man walking on the road AB takes a turn at random to reach the road ${{\rm{A}}_1}{{\rm{B}}_1}$. It is known that he reaches the road ${{\rm{A}}_1}{{\rm{B}}_1}$ from O by taking a straight line path. The chance that he moves on a straight line from the road AB to ${{\rm{A}}_1}{{\rm{B}}_1}$ is
(a) $0.25$
(b) $0.04$
(c) $0.2$
(d) None of these

Answer 1

Here, we will assume $X$ to be the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to ${{\rm{A}}_1}{{\rm{B}}_1}$. Again we will assume $Y$ to be the event that the man takes any one of the 2 straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$. We will use the formula for conditional probability to find the probability $P\left( {Y|X} \right)$, and hence, find the required chance.

Complete step by step solution:
We can observe that from AB to O, the two straight paths are from point E, and point D.
We can also observe that form O to ${{\rm{A}}_1}{{\rm{B}}_1}$, the two straight paths are from O to ${{\rm{C}}_1}$, or ${{\rm{D}}_1}$.
We will use conditional probability to find the required chance.
Let $X$ be the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to ${{\rm{A}}_1}{{\rm{B}}_1}$.
The number of ways in which the man takes any one path of the 5 paths from AB to O is given by ${}^5{C_1} = 5$ ways.
The number of ways in which the man takes any one path of the 2 straight paths from O to ${{\rm{A}}_1}{{\rm{B}}_1}$ is given by ${}^2{C_1} = 2$ ways.
Therefore, we get
The number of ways in which the man takes any one path of the 5 paths from AB to O, and then takes any one path of the 2 straight paths from O to ${{\rm{A}}_1}{{\rm{B}}_1}$ is given by $5 \times 2 = 10$ ways.
Thus, we get
$P\left( X \right) = 10$
The straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$ are the paths ${\rm{D}}{{\rm{C}}_1}$ and ${\rm{E}}{{\rm{D}}_1}$.
Let $Y$ be the event that the man takes any one of the 2 straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$.
The number of ways in which the man takes any one path of the 2 straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$ is given by ${}^2{C_1} = 2$ ways.
Therefore, we get
$P\left( Y \right) = 2$
Now, we need to find the intersection of the events $X$ and $Y$.
The event $X$ is the event that the man takes any of the 5 paths from AB to O, and then takes one of the two straight paths from O to ${{\rm{A}}_1}{{\rm{B}}_1}$.
The event $Y$ is the event that the man takes any one of the 2 straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$.
Therefore, the intersection of the events $X$ and $Y$ is the event that the man takes one of the two straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$.
The number of ways in which the man takes any one path of the 2 straight paths from AB to ${{\rm{A}}_1}{{\rm{B}}_1}$ is given by ${}^2{C_1} = 2$ ways.
Therefore, we get
$P\left( {X \cap Y} \right) = 2$
Using the formula for conditional probability, we get
$\Rightarrow P\left( {Y|X} \right) = \dfrac{{P\left( {Y \cap X} \right)}}{{P\left( X \right)}}$
Rewriting the expression, we get
$\Rightarrow P\left( {Y|X} \right) = \dfrac{{P\left( {X \cap Y} \right)}}{{P\left( X \right)}}$
Substituting $P\left( X \right) = 10$ and $P\left( {X \cap Y} \right) = 2$ in the formula, we get
$\Rightarrow P\left( {Y|X} \right) = \dfrac{2}{{10}}$
Therefore, we get
$\Rightarrow P\left( {Y|X} \right) = 0.2$
Thus, given that the man reaches the road ${{\rm{A}}_1}{{\rm{B}}_1}$ from O by taking a straight line path, the chance that he moves on a straight line from the road AB to ${{\rm{A}}_1}{{\rm{B}}_1}$ is the chance is $0.2$.

The correct option is option (c).

Note:
We used the formula for conditional probability to solve the problem. If it is given that an event $B$ has happened, then the probability that $A$ occurs after the happening of the event $B$ is given by the conditional probability $P\left( {A|B} \right) = \dfrac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}}$.