Question

The adjoining diagram shows the spectral energy density distribution ${E_\lambda }$ of black body at two different temperatures. If the area under the curves are in the ratio $16:1$, the value of temperature $T$ is

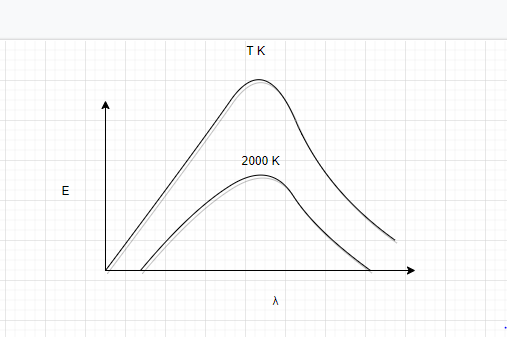
A. $32000\,K$
B. $16000\,K$
C. $8000\,K$
D. $4000\,K$

Answer 1

For a blackbody the relation between emissive power and temperature is given by Stefan’s law which states that emissive power is directly proportional to the fourth power of temperature.
$E \propto {T^4}$
Where, $E$ is the emissive power and $T$ is the temperature.
The area under the graph between energy density ${E_\lambda }$ and wavelength $\lambda$ gives the emissive power.

Complete step by step answer:
For a blackbody the relation between emissive power and temperature is given by Stefan’s law which states that emissive power is directly proportional to the fourth power of temperature.
$E \propto {T^4}$
Where, $E$ is the emissive power and $T$ is the temperature
The area under the graph between energy density ${E_\lambda }$ and wavelength $\lambda$ gives the emissive power.
Let the area under the curve at $T\,K$ be ${A_1}$.Then
${A_1} \propto {T^4}$ …… (1)
That is,${A_1} = \sigma {T^4}$
Let area under the curve at $2000\,K$ be ${A_2}$ ;then,
${A_2} \propto {\left( {2000} \right)^4}$ …….. (2)
That is,
${A_2} = \sigma {\left( {2000} \right)^4}$
Divide equation (1) by (2)
$\dfrac{{{A_1}}}{{{A_2}}} = \dfrac{{{T^4}}}{{{{\left( {2000} \right)}^4}}}$ ……. (3)
Ratio of area is given as $16:1$
Substituting this in equation (3), we get
$\dfrac{{16}}{1} = \dfrac{{{T^4}}}{{{{2000}^4}}} \\\ \left( {\dfrac{T}{{2000}}} \right) = {\left( {16} \right)^{\dfrac{1}{4}}} \\\ T = 2000 \times 2 \\\ = 4000K \\\$
So, the correct answer is option D.

Note: A black body is a body that absorbs all the radiation falling on it and it has emissivity equal to 1. It is important in this problem that we consider the power of the temperature and just don’t solve it assuming a linear relationship.