Question
Question: The adjacent figure shows charged spherical shells A, B and C having charge densities $\sigma$, -$\s...
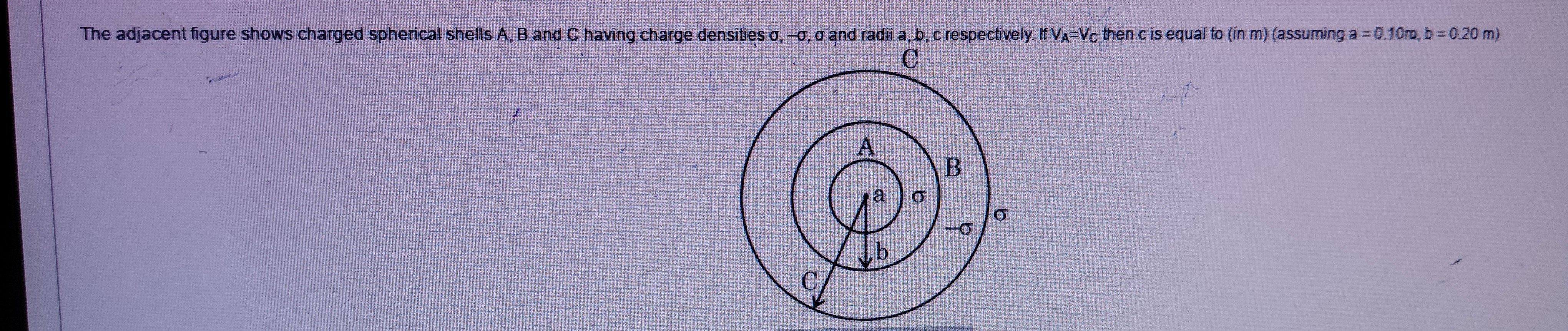
The adjacent figure shows charged spherical shells A, B and C having charge densities σ, -σ, σ and radii a, b, c respectively. If VA=VC then c is equal to (in m) (assuming a = 0.10m, b = 0.20 m)
0.30
Solution
The potential at the surface of a charged spherical shell of radius R and charge Q is given by V=4πϵ01RQ. The potential at a distance r from the center due to a charged spherical shell of radius R and charge Q is 4πϵ01rQ for r≥R and 4πϵ01RQ for r≤R.
The charges on the shells A, B, and C are QA=4πa2σ, QB=4πb2(−σ), and QC=4πc2σ, respectively.
The potential at the surface of shell A (r=a) is the sum of the potentials due to shells A, B, and C at r=a.
VA=VA on A+VB on A+VC on A
VA on A=4πϵ01aQA=4πϵ01a4πa2σ=ϵ0σa
Since a<b, the potential due to shell B at r=a is the same as the potential on the surface of B.
VB on A=4πϵ01bQB=4πϵ01b−4πb2σ=−ϵ0σb
Since a<c, the potential due to shell C at r=a is the same as the potential on the surface of C.
VC on A=4πϵ01cQC=4πϵ01c4πc2σ=ϵ0σc
So, VA=ϵ0σa−ϵ0σb+ϵ0σc=ϵ0σ(a−b+c).
The potential at the surface of shell C (r=c) is the sum of the potentials due to shells A, B, and C at r=c.
VC=VA on C+VB on C+VC on C
Since c>a, the potential due to shell A at r=c is the same as the potential at a distance c from the center.
VA on C=4πϵ01cQA=4πϵ01c4πa2σ=ϵ0cσa2
Since c>b, the potential due to shell B at r=c is the same as the potential at a distance c from the center.
VB on C=4πϵ01cQB=4πϵ01c−4πb2σ=−ϵ0cσb2
VC on C=4πϵ01cQC=4πϵ01c4πc2σ=ϵ0σc
So, VC=ϵ0cσa2−ϵ0cσb2+ϵ0σc=ϵ0σ(ca2−b2+c).
Given VA=VC:
ϵ0σ(a−b+c)=ϵ0σ(ca2−b2+c)
Assuming σ=0, we can cancel ϵ0σ:
a−b+c=ca2−b2+c
a−b=ca2−b2
c(a−b)=a2−b2
c(a−b)=(a−b)(a+b)
Since the radii are distinct (a<b<c), a=b, so a−b=0. We can divide by (a−b):
c=a+b
We are given a=0.10m and b=0.20m.
c=0.10m+0.20m=0.30m.
