Question
Question: The adjacent figure shows a non-uniform metre stick \(AB\) having the linear mass density variation ...
The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at end A and force F is applied perpendicular to the rod at the other end B and in the Second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at point A. If in the first case the angular acceleration is αA and in the second case its αB then,
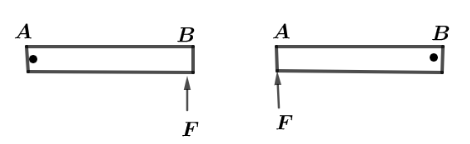
A. αA=αB
B. αA>αB
C. αA<αB
D. Data is insufficient to determine
Solution
In mechanics, when a perpendicular force is applied to the length of a given rod, it produced a rotational torque hence produce angular acceleration which depends upon the moment of inertia of the rod as, τ=Iα . where, τ is the torque acting on the rod due to force acting on it, α is the angular acceleration and I is the moment of inertia about the rotational axis. Here, we will compare the torque acting on both cases and then find the relation between angular accelerations produced in both cases.
Formula used:
The torque acting on a rod of length say L and perpendicular force F to the length is given by,
τ=FL
Moment of inertia of a rod of mass m at a perpendicular distance from axes of rotation r is given by,
I=mr2
Complete step by step answer:
Since, the length of rod and the applied perpendicular force F is same in both cases, so the torque acting in both cases will be,
τA=τB=FL
⇒τA=τB
Now, in the first case when force is applied at end B, let’s assume the moment of inertia will be IA and the angular acceleration αA . It’s given to us that linear mass density varies as λ=λ0x which means, as we will move from one end to another end of the rod the mass of the rod will increase such that, mass distribution is far for rotation about point A and mass distribution is less for rotation about point B, which means distance from ends point to axes of rotation will be rA>rB.
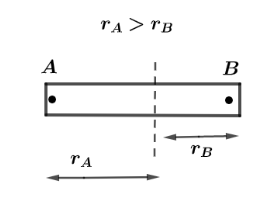
Let us assume that when force is applied at end B, the mass of the rod is mA such that the moment of inertia in the first case will be, IA=mrA2. Now, in the second case, the moment of inertia about point B can be written as IB=mrB2 .
Since, rA>rB
IA>IB
⇒IBIA>1
Now, as we have τA=τB
IAαA=IBαB
⇒IBIA=αBαA
From relation, IBIA>1 we have,
αBαA>1
Which shows that,
∴αA>αB
Hence, the correct option is B.
Note: It should be remembered that, it’s just the mass distribution which is increasing as one moves from one end to another but total mass remains constant and due to varying mass distribution the distance from action point to the axes of rotation is different in both cases which produce different angular acceleration in both cases even when total mass and length of the rod is same in both cases.
