Question

The acute angle between two straight lines passing through the point M(-6,-8) and the points in which the line segment 2x + y + 10 = 0 enclosed between the coordinate axes is divided in the ratio 1 : 2 : 2 in the direction from the point of its interaction with the x-axis to the point of intersection with the y-axis is
(A) $\dfrac{\pi }{3}$
(B) $\dfrac{\pi }{4}$
(C) $\dfrac{\pi }{6}$
(D) $\dfrac{\pi }{12}$

Answer 1

Find the coordinates of point B and C by using the formula of point of division as B divides the line AD in ratio 1:4 internally and C divides the line AD in the ratio 3:2 internally. Then find the slopes ${{m}_{1}}$ and ${{m}_{2}}$ of the lines CM and BM respectively using the formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ where ${{x}_{1}}$, ${{x}_{2}}$, ${{y}_{1}}$, ${{y}_{2}}$ are the coordinates of respective points. Find the angle $\theta$ made by the slopes ${{m}_{1}}$ and ${{m}_{2}}$ using the formula $\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$ to get the final answer.

Complete step-by-step answer:
Given that the straight line passes through the point M (-6,-8). The line segment 2x + y + 10 = 0 enclosed between the coordinate axes is divided in the ratio 1 : 2 : 2.

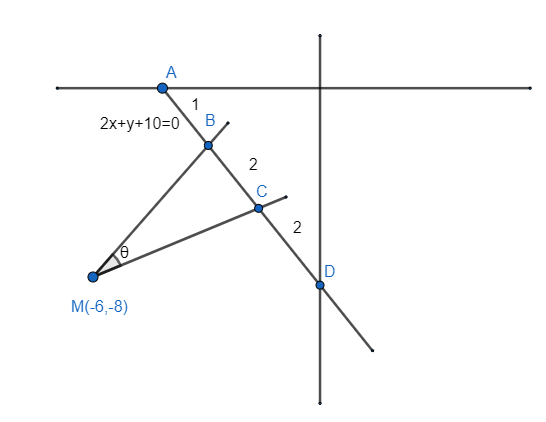
First we have to find the coordinates of B and C.
The coordinates of A and D are given by the line intercept form.
Line intercept form is $\dfrac{x}{a}+\dfrac{y}{b}=1$
The line intercept form for the line 2x + y + 10 = 0 is $\dfrac{x}{-5}+\dfrac{y}{-10}=1$
The coordinates of A and D are (-5,0) and (0,-10) respectively.
Formula: Any point P which divides the line segment joining the points A $\left( {{x}_{1}},{{y}_{1}} \right)$, B $\left( {{x}_{2}},{{y}_{2}} \right)$in the ratio m:n internally is given by
$P=\left( \dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)$
Similarly B divides AD in the ratio 1 : 4 internally. From the above formula we get point B as,
$B=\left[ \dfrac{1\left( 0 \right)+4\left( -5 \right)}{1+4},\dfrac{1\left( -10 \right)+4\left( 0 \right)}{1+4} \right]$
$B=\left( -4,-2 \right)$
Similarly C divides AD in the ratio 3 : 2 internally. From the above formula we get point C as,
$C=\left[ \dfrac{3\left( 0 \right)+2\left( -5 \right)}{3+2},\dfrac{3\left( -10 \right)+2\left( 0 \right)}{3+2} \right]$
$C=\left( -2,-6 \right)$

For line CM the coordinates are $\left( -2,-6 \right)$ and $\left( -6,-8 \right)$.
Slope of line CM is ${{m}_{1}}=\dfrac{-8+2}{-6+4}=3$

For line BM the coordinates are $\left( -4,-2 \right)$ and $\left( -6,-8 \right)$.
Slope of line BM is ${{m}_{2}}=\dfrac{-8+6}{-6+2}=\dfrac{1}{2}$
The formula for finding the angle from slopes is $\tan \theta =\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}}$

& \tan \theta =\dfrac{3-\dfrac{1}{2}}{1+\dfrac{3}{2}} \\\ & \tan \theta =1 \end{aligned}$$ That means $$\theta =\dfrac{\pi }{4}$$ **So, the correct answer is “Option B”.** **Note:** As the formulas play a key role in this problem they should be handy. As there are 4 points on the same line and the points divide the line in different ratios, be careful in writing all those. From the slopes angle is calculated using the formula of $$\tan \theta $$.