Question

The acute angle between the curves $y = \left| {{x^2} - 1} \right|$ and $y = \left| {{x^2} - 3} \right|$ at their points of intersection when $x > 0$ .

Answer 1

Here, you can roughly draw the graph to get the acute angle between the curves and where both of the graphs intersects. They draw a tangent line to get the point of intersection and then find the slope and the equation of the straight line. Remember $x > 0$ .

Formula used: For finding the slope we will find $\dfrac{{dy}}{{dx}} = m$ , for equation of straight line $y - {y_1} = m\left( {x - {x_1}} \right)$ , acute angle between the curves $\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$.

Complete step by step solution:
We will first draw the graphs for $y = \left| {{x^2} - 1} \right|$ and $y = \left| {{x^2} - 3} \right|$ for $x > 0$ in a single graph. So, that both the graphs intersect each other and draw the tangents on the graph.

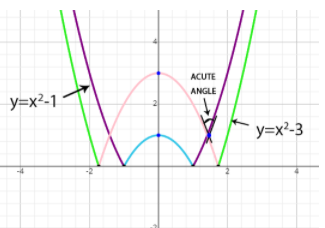
As, it is clear $x > 1$ So, $y = {x^2} - 1$ and $x < \sqrt 3$ so modulus of $y = \left| {{x^2} - 3} \right|$ will open negative. As, $y = - \left( {{x^2} - 3} \right)$ .
Comparing both the equations and calculating point of intersection.

\Rightarrow {x^2} - 1 = $$$$ - \left( {{x^2} - 3} \right)
Self Made

\Rightarrow {x^2} - 1 = $$$$ - {x^2} + 3
On Simplifying,
$\Rightarrow 2{x^2} = 4$
$\Rightarrow {x^2} = 2$
We get $x = \sqrt 2$
Putting $x = \sqrt 2$ in $y = {x^2} - 1$
$\therefore y = 1$
So, point of intersection are: $\left( {\sqrt 2 ,1} \right)$
Firstly, we will calculate slope for $y = {x^2} - 1$
$\dfrac{{dy}}{{dx}} = 2x$
Put $x = \sqrt 2$
We get,
$\dfrac{{dy}}{{dx}} = 2\sqrt 2 = {m_1}$
secondly, we will calculate slope for $y = - {x^2} + 3$
$\dfrac{{dy}}{{dx}} = - 2x$
Put $x = \sqrt 2$
We get,
$\dfrac{{dy}}{{dx}} = - 2\sqrt 2 = {m_2}$
Now we will calculate equation of straight line using formula $y - {y_1} = m\left( {x - {x_1}} \right)$
For equation 1 ${m_1} = 2\sqrt 2$ and $\left( {{x_1},{y_1}} \right) = \left( {\sqrt 2 ,1} \right)$
$y - 1 = 2\sqrt 2 \left( {x - \sqrt 2 } \right)$

For equation 2 ${m_2} = - 2\sqrt 2$ and $\left( {{x_1},{y_1}} \right) = \left( {\sqrt 2 ,1} \right)$
$y - 1 = - 2\sqrt 2 \left( {x - \sqrt 2 } \right)$
Now, we will calculate the angle between the curves using the formula $\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right|$ where ${m_1} = 2\sqrt 2$ and ${m_2} = - 2\sqrt 2$
$\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{2\sqrt 2 - \left( { - 2\sqrt 2 } \right)}}{{1 + \left( {2\sqrt 2 } \right)\left( { - 2\sqrt 2 } \right)}}} \right|$
On simplifying we get,
$\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{2\sqrt 2 + 2\sqrt 2 }}{{1 - \left( {2\sqrt 2 } \right)\left( {2\sqrt 2 } \right)}}} \right|$
$\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{4\sqrt 2 }}{{1 - 8}}} \right|$
Hence, we get $\tan \left( {\theta - {\theta _1}} \right) = \left| {\dfrac{{4\sqrt 2 }}{{ - 7}}} \right|$
As, modulus is there so it will open as a positive sign.

$\tan \left( {\theta - {\theta _1}} \right) = \dfrac{{4\sqrt 2 }}{7}$
So, $\left( {\theta - {\theta _1}} \right) = {\tan ^{ - 1}}\left( {\dfrac{{4\sqrt 2 }}{7}} \right)$ i.e $\left( {\theta - {\theta _1}} \right)$ = angle between the curves

Note:
As in these types of questions we must remember that from a graph we can easily calculate the point of intersection and we have to draw two tangents and write the equation accordingly and the equations make the straight line and hence an acute angle can be calculated when $x > 0$.