Question

The acceleration of this particle for $\left| x \right|>{{X}_{0}}$ is proportional to
A. ${{V}_{0}}$
B. $\sqrt{\dfrac{{{V}_{0}}}{m{{X}_{0}}}}$
C. $\dfrac{{{V}_{0}}}{m{{X}_{0}}}$
D. zero

Answer 1

When a particle moves in a potential of the form $V(x)=k{{x}^{n}}$. It performs simple harmonic motion. Simple harmonic motion can be defined as a periodic oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position.
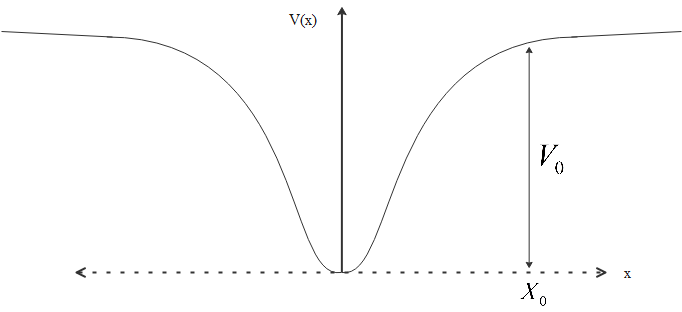
We need to study this graph and answer this question accordingly.

Complete answer:
From this graph it can be noted that potential varies with position of the particle as
V(x)=\left\\{ \begin{aligned} & \begin{matrix} k{{x}^{4}} & \text{if }0<\left| x \right|<{{X}_{0}} \\\ \end{matrix} \\\ & \begin{matrix} {{V}_{0}} & \text{Otherwise} \\\ \end{matrix} \\\ \end{aligned} \right.
Force acting on a particle moving under a potential is the negative gradient of the potential. Therefore, we get
F(x)=\left\\{ \begin{aligned} & \begin{matrix} -4k{{x}^{3}} & \text{if }0<\left| x \right|<{{X}_{0}} \\\ \end{matrix} \\\ & \begin{matrix} 0 & \text{Otherwise} \\\ \end{matrix} \\\ \end{aligned} \right.
Force on a particle is also defined as a product of its mass and acceleration. That is,
$F=ma$
Therefore acceleration of the particle can be written as,
$a=\dfrac{F}{m}$
Acceleration of particle at $\left| x \right|>{{X}_{0}}$
$a=\dfrac{F(>{{X}_{0}})}{m}$
Since, force acting on the particle at $\left| x \right|>{{X}_{0}}$ is zero. Therefore,
$\Rightarrow a=0$

So, the correct answer is “Option D”.

Additional Information:
Simple harmonic motion can be defined as a periodic oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position.
Oscillatory motion is the to and fro motion of a particle about its mean position. This means force always acts towards the mean position.
When potential is constant, no force acts on the particle. Hence, acceleration is zero.

Note:
During a SHM, the force acting on a particle is always towards the mean position or equilibrium position.
The force on a particle is zero when it reaches equilibrium position and maximum when it is at a distance equal to its amplitude. Amplitude of a SHM is the maximum distance of a particle as measured from its equilibrium position.