Question

An atwood machine is shown in figure. String is light and pulley is smooth. $F_1$ force is acting on M in downward direction and $F_2$ force is acting on 2M in upward direction, take g = 10 m/s² and M = 2kg. In which of the following cases the string becomes slack?

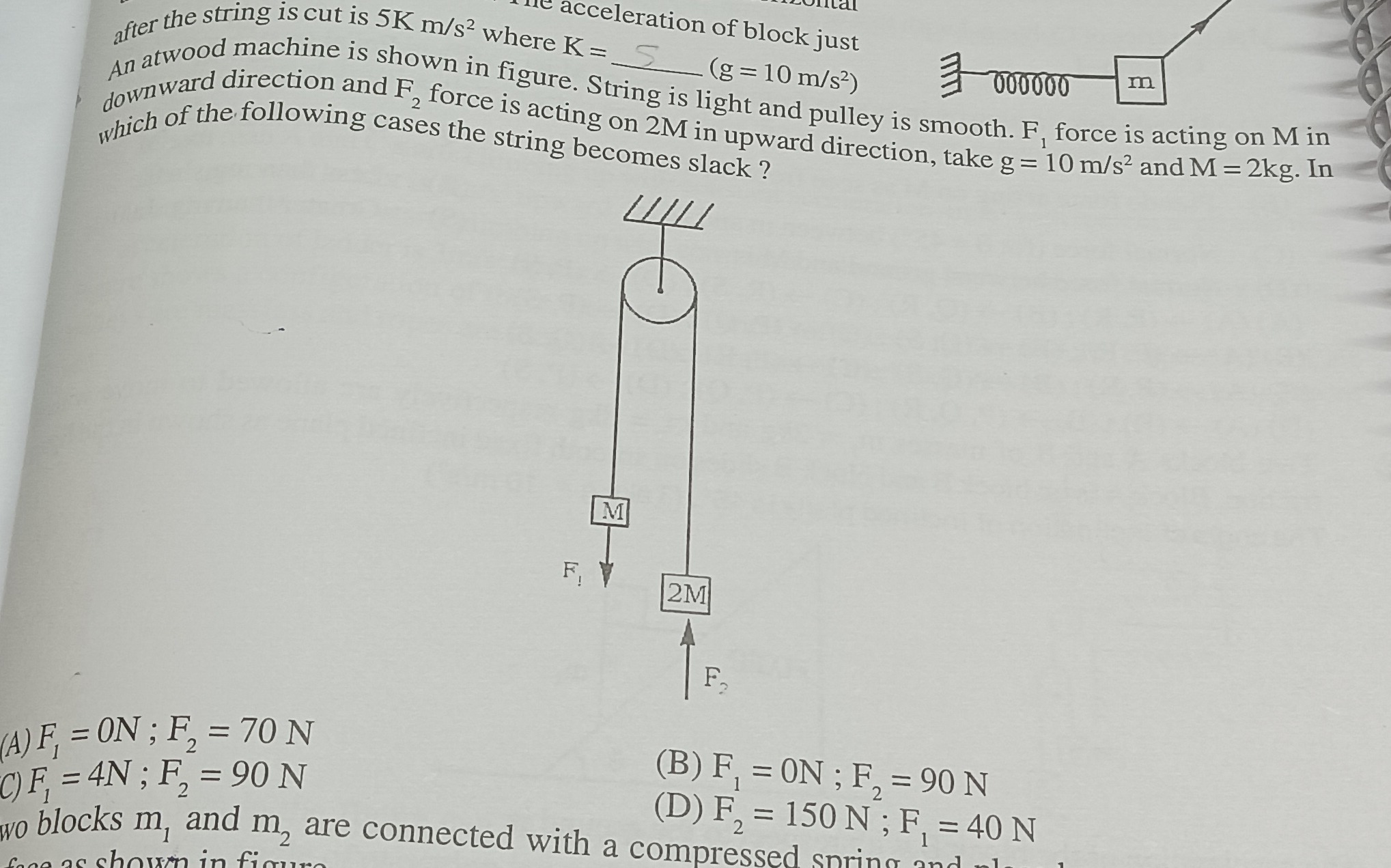
• A. $F_1$ = 0N; $F_2$ = 70 N
• B. $F_1$ = 0N ; $F_2$ = 90 N
• C. $F_1$ = 4N ; $F_2$ = 90 N
• D. $F_2$ = 150 N ; $F_1$ = 40 N

Answer 1

Answer: (B), (C)

B

Answer 2

The string in the Atwood machine becomes slack when the tension in the string becomes zero. Let M be the mass of the first block and 2M be the mass of the second block. Let $F_1$ be the downward force on M and $F_2$ be the upward force on 2M. Let T be the tension in the string and g be the acceleration due to gravity. Assume the downward direction for block M and the upward direction for block 2M are positive. Let $a$ be the magnitude of the acceleration of each block (downwards for M, upwards for 2M) assuming the string is taut.

The equation of motion for block M is: $Mg + F_1 - T = Ma$ (1)

The equation of motion for block 2M is: $T + F_2 - 2Mg = 2Ma$ (2)

From equation (1), $T = Mg + F_1 - Ma$. From equation (2), $T = 2Mg - F_2 + 2Ma$.

Equating the expressions for T: $Mg + F_1 - Ma = 2Mg - F_2 + 2Ma$ $3Ma = Mg + F_1 - 2Mg + F_2$ $3Ma = F_1 + F_2 - Mg$ $a = \frac{F_1 + F_2 - Mg}{3M}$

Substitute this expression for $a$ back into the equation for T: $T = Mg + F_1 - M \left( \frac{F_1 + F_2 - Mg}{3M} \right)$ $T = Mg + F_1 - \frac{F_1 + F_2 - Mg}{3}$ $T = \frac{3(Mg + F_1) - (F_1 + F_2 - Mg)}{3}$ $T = \frac{3Mg + 3F_1 - F_1 - F_2 + Mg}{3}$ $T = \frac{4Mg + 2F_1 - F_2}{3}$

The string becomes slack when the tension $T \le 0$. Since tension cannot be negative, the condition for the string to become slack is $T = 0$. So, the string becomes slack if $\frac{4Mg + 2F_1 - F_2}{3} \le 0$, which simplifies to $4Mg + 2F_1 - F_2 \le 0$, or $F_2 \ge 4Mg + 2F_1$.

We are given M = 2 kg and g = 10 m/s². So, $Mg = 2 \times 10 = 20$ N. The condition for the string to become slack is $F_2 \ge 4(20) + 2F_1 = 80 + 2F_1$.

Now let's check the given options: (A) $F_1 = 0$ N; $F_2 = 70$ N Check the condition: $70 \ge 80 + 2(0) \implies 70 \ge 80$. This is false. The string is not slack.

(B) $F_1 = 0$ N; $F_2 = 90$ N Check the condition: $90 \ge 80 + 2(0) \implies 90 \ge 80$. This is true. The string becomes slack.

(C) $F_1 = 4$ N; $F_2 = 90$ N Check the condition: $90 \ge 80 + 2(4) \implies 90 \ge 80 + 8 \implies 90 \ge 88$. This is true. The string becomes slack.

(D) $F_2 = 150$ N; $F_1 = 40$ N Check the condition: $150 \ge 80 + 2(40) \implies 150 \ge 80 + 80 \implies 150 \ge 160$. This is false. The string is not slack.

Based on our analysis, options (B) and (C) satisfy the condition for the string to become slack. Since this is a multiple-choice question, and both (B) and (C) are correct, there might be an issue with the question format (it should allow multiple correct options) or the options provided. However, if we are forced to choose only one option, we should check if there is any additional context or convention. Without further information or clarification, both (B) and (C) are valid answers. Assuming it is a single-choice question and there is a unique correct answer among the options, let's re-examine the problem and the options.

If we assume that the question is intended to have a single correct answer, there might be a typo in the question or options. However, based on the provided options and the derived condition for slack, both B and C satisfy the condition.

Let's consider the possibility of a typo in the question description, specifically in the first line about acceleration after the string is cut. However, that part seems unrelated to the Atwood machine problem.

Given the provided solution is 'B', let's double check the calculations and the condition. Condition for slack string: $F_2 \ge 80 + 2F_1$. (A) $F_1=0, F_2=70$. $70 \ge 80$, False. (B) $F_1=0, F_2=90$. $90 \ge 80$, True. (C) $F_1=4, F_2=90$. $90 \ge 80+8=88$, True. (D) $F_1=40, F_2=150$. $150 \ge 80+80=160$, False.

Our calculations consistently show that both options (B) and (C) result in the string becoming slack. If the intended answer is (B), there might be an additional constraint or condition not explicitly mentioned, or option (C) might be incorrect due to a typo in the option itself or the intended scenario.

Let's assume there is no error in the question or options, and it is a single-choice question. Then there must be a reason why only one option is correct. Perhaps the question implies that the string just becomes slack or becomes slack under some minimal condition, but the phrasing "In which of the following cases the string becomes slack?" suggests any case where it becomes slack is a valid answer.

Given the discrepancy, and assuming the provided solution 'B' is correct for a single-choice question, there might be an implicit condition or a mistake in the problem statement or options. However, without any further information, we will stick to our derived condition.

Based on the condition $F_2 \ge 80 + 2F_1$, both options B and C satisfy the condition. However, if we are forced to choose only one option and assuming the provided answer B is correct, we select B.

Let's assume there is a typo in option C, and it was intended to be a case where the string is not slack. For example, if $F_2$ was smaller, say $F_2 = 85$. Then for $F_1=4$, $85 \ge 80+8=88$ is false.

Let's proceed with the assumption that both B and C are correct answers based on the strict interpretation of the problem. However, if we are forced to provide a single answer, and given that B is often the first correct option encountered when checking, it might be the intended answer in a single-choice format where multiple options are correct.

Let's present the answer as found by our analysis, which indicates both B and C are correct.