Question

An atwood machine is shown in figure. String is light and pulley is smooth. $F_1$ force is acting on M in downward direction and $F_2$ force is acting on 2M in upward direction, take g = 10 m/s² and M = 2kg. In which of the following cases the string becomes slack?

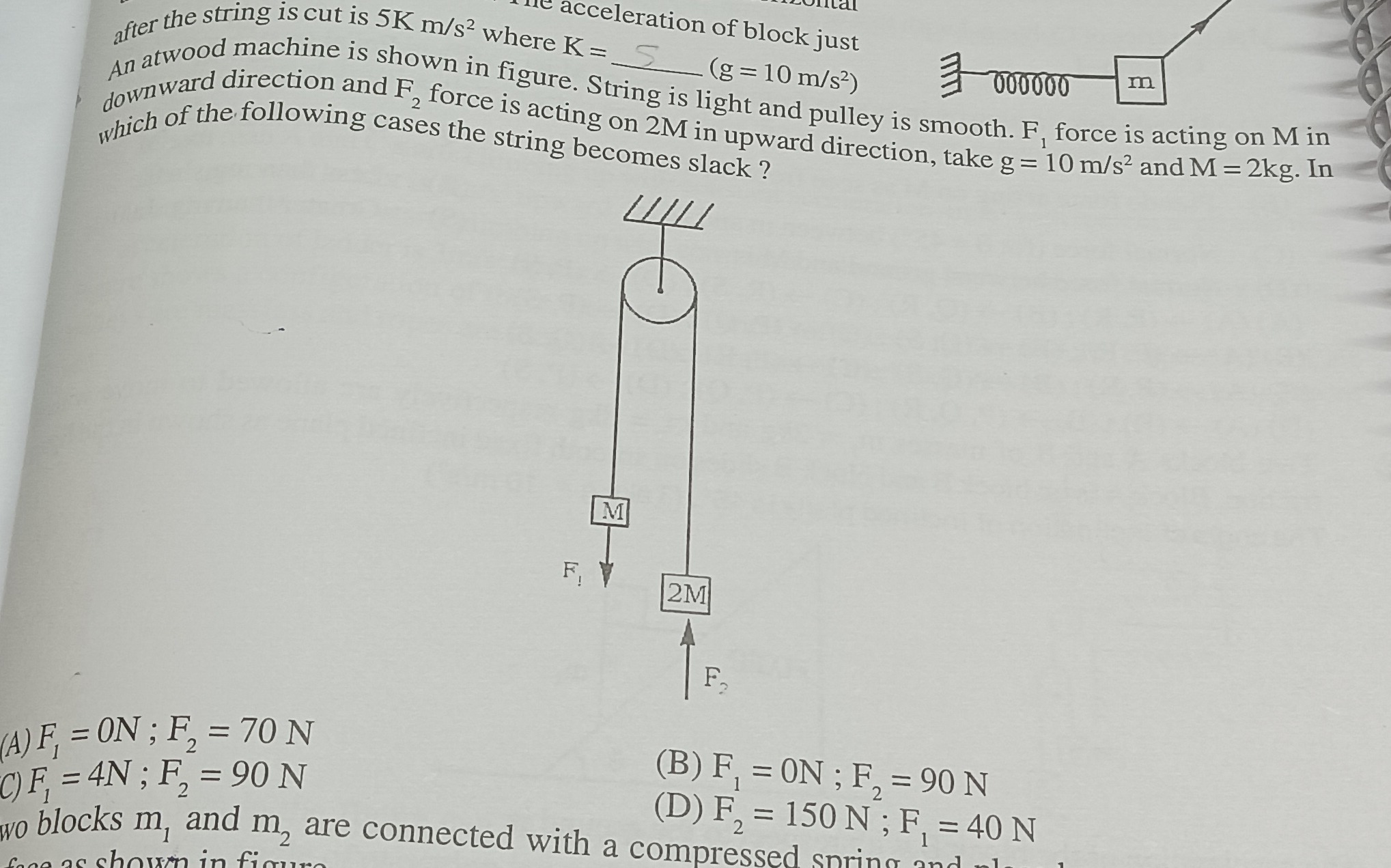
• A. $F_1$ = 0N; $F_2$ = 70 N
• B. $F_1$ = 0N ; $F_2$ = 90 N
• C. $F_1$ = 4N ; $F_2$ = 90 N
• D. $F_2$ = 150 N ; $F_1$ = 40 N

Answer 1

Answer: (B), (C)

(B), (C)

Answer 2

The string in an Atwood machine becomes slack when the tension in the string is zero.

Let T be the tension in the string. Let M be the mass on the left side and 2M be the mass on the right side. A downward force $F_1$ acts on M, and an upward force $F_2$ acts on 2M. Let's assume that mass M moves downwards with acceleration $a$ and mass 2M moves upwards with acceleration $a$.

The forces acting on mass M are its weight Mg downwards, the applied force $F_1$ downwards, and the tension T upwards. The equation of motion for mass M is:

$Mg + F_1 - T = Ma$ (1)

The forces acting on mass 2M are its weight 2Mg downwards, the applied force $F_2$ upwards, and the tension T upwards. The equation of motion for mass 2M is:

$T + F_2 - 2Mg = 2Ma$ (2)

We can solve for the tension T from these two equations. From equation (1), $T = Mg + F_1 - Ma$. Substitute this into equation (2):

$(Mg + F_1 - Ma) + F_2 - 2Mg = 2Ma$

$F_1 + F_2 - Mg = 3Ma$

$a = \frac{F_1 + F_2 - Mg}{3M}$

Now substitute the expression for $a$ back into the expression for T:

$T = Mg + F_1 - M \left( \frac{F_1 + F_2 - Mg}{3M} \right)$

$T = Mg + F_1 - \frac{F_1 + F_2 - Mg}{3}$

$T = \frac{3(Mg + F_1) - (F_1 + F_2 - Mg)}{3}$

$T = \frac{3Mg + 3F_1 - F_1 - F_2 + Mg}{3}$

$T = \frac{4Mg + 2F_1 - F_2}{3}$

The string becomes slack when the tension $T \le 0$. Since tension cannot be negative in a string, the condition for the string to become slack is $T = 0$. However, if the calculation gives a negative tension, it implies that the string is not needed to maintain the assumed motion, and thus the string will be slack (tension will be zero). So, the condition for the string to become slack is $T \le 0$.

$\frac{4Mg + 2F_1 - F_2}{3} \le 0$

$4Mg + 2F_1 - F_2 \le 0$

$F_2 \ge 4Mg + 2F_1$

We are given M = 2 kg and g = 10 m/s². So Mg = 2 * 10 = 20 N.

The condition for the string to become slack is $F_2 \ge 4(20) + 2F_1$, which simplifies to $F_2 \ge 80 + 2F_1$.

Now let's check each option:

(A) $F_1 = 0$ N; $F_2 = 70$ N

Check if $F_2 \ge 80 + 2F_1$: $70 \ge 80 + 2(0) = 80$. This is false ($70 < 80$). The string is not slack.

(B) $F_1 = 0$ N; $F_2 = 90$ N

Check if $F_2 \ge 80 + 2F_1$: $90 \ge 80 + 2(0) = 80$. This is true ($90 \ge 80$). The string becomes slack.

(C) $F_1 = 4$ N; $F_2 = 90$ N

Check if $F_2 \ge 80 + 2F_1$: $90 \ge 80 + 2(4) = 80 + 8 = 88$. This is true ($90 \ge 88$). The string becomes slack.

(D) $F_2 = 150$ N; $F_1 = 40$ N

Check if $F_2 \ge 80 + 2F_1$: $150 \ge 80 + 2(40) = 80 + 80 = 160$. This is false ($150 < 160$). The string is not slack.

The string becomes slack in cases (B) and (C).