Question

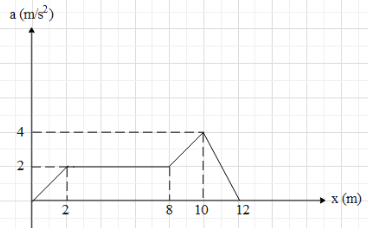
The acceleration-displacement graph of particles moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is $x=12cm$.

A. $4\sqrt{3}m{{s}^{-1}}$
B. $4\sqrt{2}m{{s}^{-1}}$
C. $2\sqrt{3}m{{s}^{-1}}$
D. $2\sqrt{2}m{{s}^{-1}}$

Answer 1

Use the definition of acceleration and velocity and derive a relation between acceleration, velocity and displacement of a particle. Then further process involves integration. Also make use of the given data from integration.

Formula used:
$a=\dfrac{dv}{dt}$
$v=\dfrac{dx}{dt}$
$W=\int{F.dx}$
$K=\dfrac{1}{2}m{{v}^{2}}$

Complete step by step answer:
We know that acceleration of a particle is the rate of change of its velocity with respect to time. Therefore, acceleration is equal to the change in velocity per unit time.The expression for acceleration (a) of a particle travelling with velocity v is given as $a=\dfrac{dv}{dt}$ …. (i)
(t is time).i.e. acceleration (a) is the first derivative of velocity with respect to time.And velocity of the particle is the rate of change in position of the particle with respect to time. In others words, velocity is equal to the displacement of the particle per unit time. Hence, velocity is the first derivative of the displacement of the particle with respect to time.
i.e. $v=\dfrac{dx}{dt}$ (ii), where x is its displacement.
Now, divide equation (i) by (ii).
$\Rightarrow \dfrac{a}{v}=\dfrac{\dfrac{dv}{dt}}{\dfrac{dx}{dt}}$
$\Rightarrow \dfrac{a}{v}=\dfrac{dv}{dx}$
$\Rightarrow a=v\dfrac{dv}{dx}$ ….. (iii).
Hence, we found a relation between acceleration, velocity and displacement of a particle.
Now, equation (iii) can be written as,
$\Rightarrow adx=vdv$
Integrate both sides of the equation. The limits of ‘x’ will range from $x=0m$ to $x=12m$.
It is given that at $x=0m$, $v=0m{{s}^{-1}}$ and let at $x=12m$, its velocity be $v$.
$\Rightarrow \int\limits_{0}^{12}{adx}=\int\limits_{0}^{v}{vdv}$
And
$\Rightarrow \int\limits_{0}^{v}{vdv}=\left. \dfrac{1}{2}{{v}^{2}} \right|_{0}^{v}=\dfrac{1}{2}({{v}^{2}}-0)=\dfrac{1}{2}{{v}^{2}}$.
$\Rightarrow \int\limits_{0}^{12}{adx}=\dfrac{1}{2}{{v}^{2}}$.
Since the given graph of acceleration-displacement graph, $\int\limits_{0}^{12}{adx}$ will be equal to the area under curve within the limits of x.
This means that $\dfrac{1}{2}{{v}^{2}}$ is equal to the area under the given curve.
From the figure, the area under the curve will be equal to $\dfrac{1}{2}(2)(2)+(6)(2)+(2)(2)+\dfrac{1}{2}(2)(2)+\dfrac{1}{2}(4)(2)=2+12+4+2+4=24{{m}^{2}}{{s}^{-2}}$.
$\Rightarrow \dfrac{1}{2}{{v}^{2}}=24$
$\Rightarrow {{v}^{2}}=48$
$\therefore v=\sqrt{48}=4\sqrt{3}m{{s}^{-1}}$

Hence, option A is the correct answer.

Note: We can also use the work-energy theorem. According to this theorem, the total work done on a particle is equal to the change in its kinetic energy.
i.e. $W=\Delta K$
The work done on a particle is equal to $W=\int{F.dx}$, where W is work done, F is the applied force in the direction of the displacement (x).
But we know that $F=ma$.
$\Rightarrow W=\int{ma.dx}=m\int{adx}$.
The kinetic energy of a particle is given as $\dfrac{1}{2}m{{v}^{2}}$. Since the particle is at rest at $x=0m$, the change in its kinetic energy is $\Delta K=\dfrac{1}{2}m{{v}^{2}}$.
This means that $m\int{adx}=\dfrac{1}{2}m{{v}^{2}}$
$\Rightarrow \int{adx}=\dfrac{1}{2}{{v}^{2}}$.