Question

The acceleration at any instant is the slope of the tangent of what curve at that instant?

Answer 1

Acceleration is defined as the rate of change of velocity with respect to time and velocity is further defined as rate of change of displacement with respect to time. Thus, there must a suitable plot for acceleration in terms of these entities, whose slope of the tangent will give us the acceleration at that instant. We shall find this curve to answer our problem.

Complete step by step answer:
The definition of acceleration is given as, the rate of change of velocity with respect to time. This can mathematically be written as:
$\Rightarrow \overrightarrow{a}=\dfrac{d\left( \overrightarrow{v} \right)}{dt}$
From our above equation, we can see that acceleration is a differential of velocity vector with respect to time. Also, the slope of tangent at any point on a curve is a differential of one entity with respect to another. Thus, if we are to plot a velocity-time graph and find the slope of the tangent at any point on the curve, we will get the same expression as above. This can be understood by the following diagram:

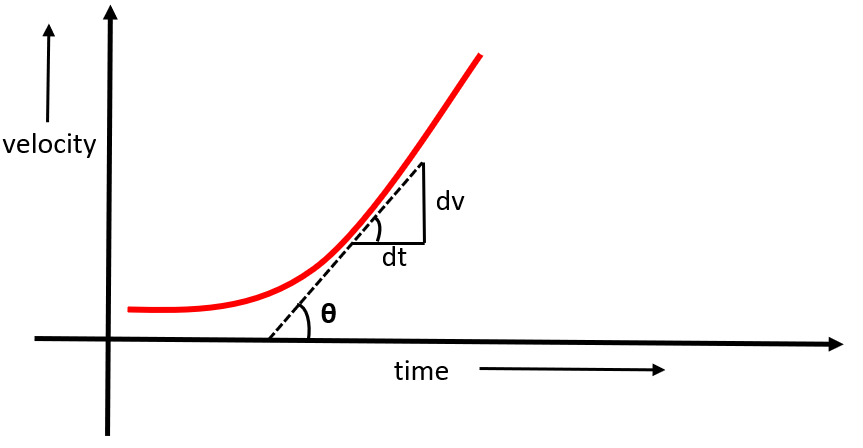
In the above diagram, we can see that the tangent of slope, that is, $\tan \theta$ is equal to $\dfrac{dv}{dt}$.Thus, we can say that the tangent of slope of velocity in a velocity-time plot gives us the acceleration.
Hence, the acceleration at any instant is the slope of the tangent of velocity-time curve at that instant.

Note: Here, we saw that acceleration at any instant is the slope of the tangent of velocity-time graph at that instant. The reverse of this could be stated as, the average velocity of a particle over a time duration can be calculated by calculating the area under the graph of the acceleration-time graph. One should be able to visualize these facts on its own for better understanding of motion of particles.