Question

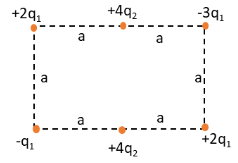
The above figure shows a rectangular array of charged particles fixed in place, with distance $a = 39.0\,{\text{cm}}$ and the charges shown as integer multiples of ${q_1} = 3.40\,{\text{pC}}$ and ${q_2} = 6.00\,{\text{pC}}$. With $V = 0$ at infinity, what is the net potential at the rectangle’s centre?

Answer 1

Use the formula for the potential at a point due to a charge. This formula gives the relation between the potential, a constant, charge and distance of the point from the charge. Determine the distance of all the charges from the centre of the rectangle and then calculate the net potential at the centre of the rectangle due to all these charges.

Formula used:
The potential $V$ due to a charge at a point is given by
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{r}$ …… (1)
Here, ${\varepsilon _0}$ is the permittivity of free space, $q$ is the charge and $r$ is the distance of charge from the point.

Complete step by step answer:
We have given the arrangement of the charges on a rectangle.We have also given that,
$a = 39.0\,{\text{cm}}$
$\Rightarrow{q_1} = 3.40\,{\text{pC}}$
$\Rightarrow{q_2} = 6.00\,{\text{pC}}$
The potential due to a charge at a distance infinity from the rectangle is zero i.e, $V = 0$.We have asked to determine the potential due to all the charges at a point at the centre of the rectangle.The four charges at the corner of the rectangle are at the same distance from the centre of the rectangle. Let $x$ be the distance of all these corner charges from the centre of the rectangle.The distance of the two charges at the middle point on the length of the rectangle is $\dfrac{a}{2}$.

The net potential at a point at the centre of the rectangle is the sum of the potentials due to all the charges on the rectangle.
$V = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ + 2{q_1}}}{x} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - {q_1}}}{x} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ + 2{q_1}}}{x} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ - 3{q_1}}}{x} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ + 4{q_2}}}{{\dfrac{a}{2}}} + \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{ + 4{q_2}}}{{\dfrac{a}{2}}}$
$\Rightarrow V = \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{ + 2{q_1} - {q_1} + 2{q_1} - 3{q_1}}}{x}} \right) + \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{ + 4{q_2}}}{{\dfrac{a}{2}}} + \dfrac{{ + 4{q_2}}}{{\dfrac{a}{2}}}} \right)$
$\Rightarrow V = \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{0}{x}} \right) + \dfrac{1}{{4\pi {\varepsilon _0}}}\left( {\dfrac{{16{q_2}}}{a}} \right)$
$\Rightarrow V = \dfrac{1}{{4\pi {\varepsilon _0}}}\left[ {\dfrac{{16{q_2}}}{a}} \right]$

Substitute $8.99 \times {10^9}\,{\text{N}} \cdot {{\text{m}}^{\text{2}}}{\text{/}}{{\text{C}}^{\text{2}}}$ for $\dfrac{1}{{4\pi {\varepsilon _0}}}$, for ${q_2}$ and $39.0\,{\text{cm}}$ for $a$ in the above equation.
$\Rightarrow V = \left( {8.99 \times {{10}^9}\,{\text{N}} \cdot {{\text{m}}^{\text{2}}}{\text{/}}{{\text{C}}^{\text{2}}}} \right)\left[ {\dfrac{{16\left( {6.00\,{\text{pC}}} \right)}}{{39.0\,{\text{cm}}}}} \right]$
$\Rightarrow V = \left( {8.99 \times {{10}^9}\,{\text{N}} \cdot {{\text{m}}^{\text{2}}}{\text{/}}{{\text{C}}^{\text{2}}}} \right)\left[ {\dfrac{{16\left( {6.00 \times {{10}^{ - 12}}\,{\text{C}}} \right)}}{{39.0 \times {{10}^{ - 2}}\,{\text{m}}}}} \right]$
$\therefore V = 2.21\,{\text{V}}$

Hence, the net potential at the centre of the rectangle is $2.21\,{\text{V}}$.

Note: One can also solve the same question by another method. One can see that the sum of all the charges at the four corners of the rectangle is zero. Hence, the potential due to these four charges must also be zero. Then one can directly calculate the net potential due to the two charges at the middle of length of the rectangle.