Question
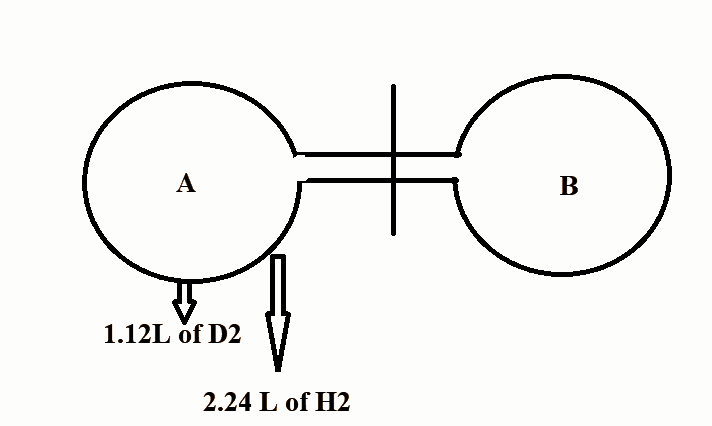
Question: The above experiment is done at NTP. The stop cock is opened for a certain time and then closed. Aft...
The above experiment is done at NTP. The stop cock is opened for a certain time and then closed. After effusion, the bulb A contains 0.1g of D2 . Find out the number of moles of H2 in bulb B.
Solution
To answer this question you should know the concept of the ideal gas equation and Graham's law of diffusion. Use graham's law of diffusion to calculate the amount of gas diffused which can be used to calculate the leftover moles.
Formula used: No. of moles = Molar mass of a SubstanceMass of the Substance in grams
rate of effusion∝molar mass of gas1
Complete step by step solution:
In the question, we are given that the volume of D2 at NTP is 1.12L.
The number of moles of D2 will be 22.41.12=0.05 moles.
Now we can calculate the mass of D2 present
⇒0.05×4=0.2g
Similarly, the mass of H2 can be calculated to be 0.1×2=0.2g
After effusion bulb A contains 0.1g of D2
Therefore, the amount of D2 effused in bulb B is 0.1g.
According to Graham’s law:
rate of effusion∝molar mass of gas1
Therefore, the relation between rates and molar mass can be written as:
rD2rH2=MH2MD2=wD2wH2
Substituting the appropriate values, we will get the value:
wH2=24×0.1=0.14g
This is the amount of H2 in bulb B.
Now, the moles of H2 will be 20.14=0.07 moles.
Note: Make sure you remember that at conditions of high temperature and lower pressure, a real gas behaves like an ideal gas, because the potential energy due to intermolecular attractive forces becomes less significant compared with the particles’ kinetic energy, and the size of the molecules becomes less significant compared to the space between them. The five gas laws are:
1.Boyle’s Law establishes a relationship between the pressure and the volume of a gas.
2.Charles’s Law establishes a relationship between the volume occupied by a gas and the absolute temperature.
3.Gay-Lussac’s Law establishes a relationship between the pressure exerted by a gas on the walls of its container and the absolute temperature associated with the gas.
4.Avogadro’s Law establishes a relationship between the volume occupied by a gas and the amount of gaseous substance.
5.After combining these four aforementioned laws we arrive at the Combined Gas Law
