Question
Question: The \( ABC \) is a triangular plate of uniform thickness. The sides are in the ratio shown in the fi...
The ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plate about AB,BC and CA respectively. Then which of the following conditions/conditions will satisfy?
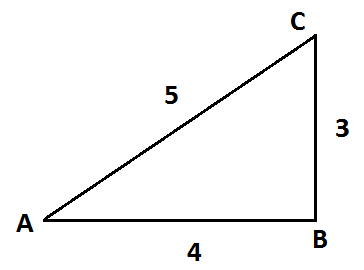
(A) IAB+IBC=ICA
(B) ICA is maximum
(C) IAB>IBC
(D) IBC>IAB
Solution
Hint : Find the moment of Inertia of the triangle about its different base and compare them.
Use the formula, the Moment of Inertia of a triangular plate about its base is, IB=6Mh2 ,Where M is the total mass of the triangular plate and h is the height about it’s any of the sides.
Complete Step By Step Answer:
We know that the Moment of Inertia of a triangular plate about its base is, IB=6Mh2 , Where M is the total mass of the triangular plate and h is the height about its any of the sides.
Here, we have a right -angle triangle, so we can find the height taking each of the sides as base easily.
Now, let’s first take AB as the base of the triangle. So, then the height of the triangle becomes BC
Therefore, Moment of Inertia about AB will be, IAB=6Mh12
Here, h1=3
∴ IAB=6M⋅32=69M
Now, let’s take BC as the base of the triangle. So, then the height of the triangle becomes AB
Therefore, Moment of Inertia about BC will be , IBC=6Mh22
Here, h2=4
∴ IBC=6M⋅42=616M
Now, take CA as the base of the triangle. Then, Moment of Inertia about CA will be ICA=6Mh32
Here, we have to calculate h3 . Now, from the figure we can find sinθ for ΔABC and also for triangle ΔBCD . So, for ΔABC , sinθ=hyp.perp.=ACAB
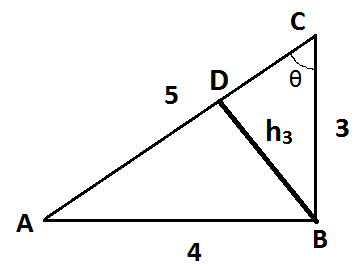
∴ sinθ=54
So, for ΔBCD , sinθ=BCBD
∴ sinθ=3h3
So, we can equate both the sinθ
Hence, equating we get, h3=53⋅4
Therefore, h3=512
Hence, ICA=6Mh32=6M(512)2=5144⋅6M
That becomes,
ICA=628.8M
Therefore we have, IAB=69M , IBC=616M and ICA=628.8M
Hence, IAB=69M<IBC=616M<ICA=628.8M
Now, we can see that IBC>IAB and we can also see that the sum of IAB and IBC is, IAB+IBC=69M+616M=625M=ICA
Therefore, Option (D ) is correct only.
Note :
∙ Calculating Moment of Inertia is a very lengthy calculation to do, so, it is advised to memorize the Moment of Inertia for different geometrical shapes for convenience.
∙ This problem can also be solved using parallel axes theorem .If we can find the distance between the centre of mass and the sides then we can compare the moment of inertia easily.
