Question
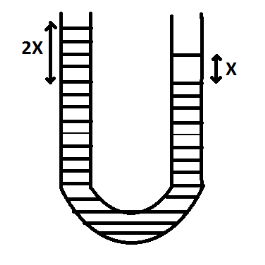
Question: The \(9kg\) solution is poured into a glass U-tube as shown in the figure below. The tube’s inner di...
The 9kg solution is poured into a glass U-tube as shown in the figure below. The tube’s inner diameter is 25πm and the solution oscillates freely up and down about its position of equilibrium(x=0). The period of oscillation in seconds is: (1m3of solution has a mass μ=900kg, g=10m/s2. Ignore frictional and surface tension effects)
A. 0.1
B. 10
C. π
D. 1
Solution
Here, we are given a mass of a solution in the volume of 1m3which can be taken as the density of the material. We can equate the mass poured in the solution with the density multiplied by the volume of the liquid which is oscillating. By this we can find the oscillation length which is further used to find the period of oscillation.
Formulas used:
V=πr2l,
where, V is the volume, r is the inner radius of tube and l is the length of oscillation
ρ=Vm ,
where, ρ is the density of the liquid, m is the mass of liquid and V is the volume of the liquid
T=2π2gl,
Where, T is the period of oscillation, l is the length of oscillation and g is the gravitational acceleration
Complete step by step answer:
We know that h
\rho = \dfrac{m}{V} \\\
\Rightarrow m = \rho V \\\
We will put m=9kg, ρ=900kg/m3and V=πr2l
⇒9=900πr2l
We are given that r=25πm
9=5900π2l ⇒l=100π25
Now, to find the period of oscillation we will use the formula:
T=2π2gl ⇒T=2π200π2×105 ∴T=0.1s
Thus, option A is the right answer.
Note: For solving this question, we have used the time period of oscillating fluid. Here we can clearly see that the time period of oscillating fluid is different from the time period of simple oscillation. To be precise, it is 21times the normal oscillation such as a simple pendulum.
