Solveeit Logo
Login

Question

Question: The \({}_{98}^{250}Cf\) is split into two parts of almost equal mass. What is the order of magnitude...

The 98250Cf{}_{98}^{250}Cf is split into two parts of almost equal mass. What is the order of magnitude for potential energy of interaction of the two parts when they are just touching each other? (in 10n eV{10^n}{\text{ }}eV). Find value of nn.

Explanation

Solution

First of all, we have to find the atomic mass of each subdivided atom.The two parts that are being split are nucleus. Then we have to find the radius of each nucleus. Then by the help of the formula to find the potential energy, we will find the answer.

Formula used:
The formula to find the potential energy between the two nucleus, when they are in touch with each other is −GMmr−−−−−(1) - \dfrac{{GMm}}{r} - - - - - \left( 1 \right) where, G=G = Universal Gravitational Constant, M=m=M = m = mass of each nucleus, r=r = distance between the centre of each nucleus.

Complete step by step answer:
Let us first consider the splitting of the atom. Let the subdivided parts be XX.Thus, we get,
98250Cf→49125X+49125X{}_{98}^{250}Cf \to {}_{49}^{125}X + {}_{49}^{125}X

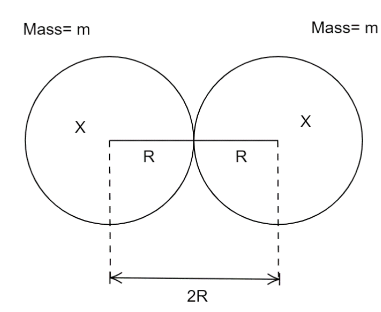
Let the radius of each nucleus be RR.
R=R0A13R = {R_0}{A^{\dfrac{1}{3}}}
where R0=1.25×10−15 m{R_0} = 1.25 \times {10^{ - 15}}{\text{ }}m is constant and A=A = atomic number.
R=1.25×10−15×(125)13R = 1.25 \times {10^{ - 15}} \times {(125)^{\dfrac{1}{3}}}
⇒R=6.25×10−15 m\Rightarrow R = 6.25 \times {10^{ - 15}}{\text{ }}m
The formula to find the potential energy between the two nucleus, when they are in touch with each other is −GMmr−−−−−(1) - \dfrac{{GMm}}{r} - - - - - \left( 1 \right) where, G=G = Universal Gravitational Constant, M=m=M = m = mass of each nucleus, r=r = distance between the centre of each nucleus.

The values of the given variables are,
G=6.67×10−11 Nkg2m2G = 6.67 \times {10^{ - 11}}{\text{ }}\dfrac{N}{{k{g^2}{m^2}}}
⇒M=m=125×1.67×10−27 kg\Rightarrow M = m = 125 \times 1.67 \times {10^{ - 27}}{\text{ }}kg
⇒r=2R=2×6.25×10−15 m\Rightarrow r = 2R = 2 \times 6.25 \times {10^{ - 15}}{\text{ }}m
Substituting all the value sin equation (1)\left( 1 \right) we get,
Potential Energy=−6.67×10−11×(125×1.67×10−27)22×6.25×10−15 J\text{Potential Energy} = - \dfrac{{6.67 \times {{10}^{ - 11}} \times {{(125 \times 1.67 \times {{10}^{ - 27}})}^2}}}{{2 \times 6.25 \times {{10}^{ - 15}}}}{\text{ }}J
⇒Potential Energy≈2.9×10−6012.5×10−15 ⇒Potential Energy≈2.3×10−46 J\Rightarrow \text{Potential Energy} \approx \dfrac{{2.9 \times {{10}^{ - 60}}}}{{12.5 \times {{10}^{ - 15}}}} \\\ \Rightarrow \text{Potential Energy}\approx 2.3 \times {10^{ - 46}}{\text{ }}J
In terms of electron Volt or eVeV we get,
Potential Energy=2.3×10−461.6×10−19 ∴Potential Energy=1.4×10−27 eV\text{Potential Energy}= \dfrac{{2.3 \times {{10}^{ - 46}}}}{{1.6 \times {{10}^{ - 19}}}} \\\ \therefore \text{Potential Energy}= 1.4 \times {10^{ - 27}}{\text{ }}eV

Thus, the order of n=−27n = - 27.

Note: It must be noted that the potential energy of a system between two charges is the same for two atoms. The mass of each nucleus is found from the atomic mass of it to the mass of each atom. In order to find anything in electron volt we must divide the following variable with the amount of charge associated with each electron.