Question

The $_{98}^{250}Cf$ is split into two parts of almost equal mass. What is the order of magnitude of potential energy of interaction of the two parts when they are just touching each other? (In ${10^n}$ eV)

Answer 1

Since the atom got split into two parts of almost equal mass, the mass of each of the daughter atoms would be half of the original atom. When the daughter atoms are just touching each other, they share a common point through which both atoms pass. And since while calculating the gravitational potential, the distance is calculated from the center of the bodies, the total effective distance would become $x = 2r$ . We will now simply plug in the values into the formula to get the order of magnitude of the potential energy.

Formula used:
The gravitational potential is given by,
$V = \dfrac{{G{m_1}{m_2}}}{x}$
where $x$ is the distance between the two bodies.

Complete step by step answer:
Let’s visualize the situation first.The diagram below shows the situation

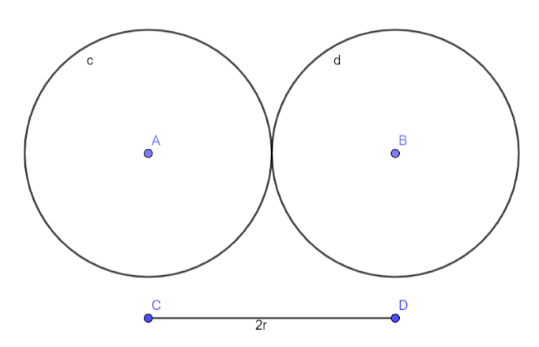
Let the radius of one of the masses be r. The distance between the centers is $x = 2r$.The mass of the given $_{98}^{250}Cf$ atom is 250. Hence the mass of each of the entities is,
$m = \dfrac{{250}}{2}$
$\Rightarrow m = 125\,g$
The gravitational potential is given by
$V = \dfrac{{G{m_1}{m_2}}}{x}$
Here it is given that ${m_1} = {m_2}$.
So, the formula reduces to $V = \dfrac{{G{m^2}}}{x}$ .

Substituting the values in the equation we get,
$V = \dfrac{{6.67 \times {{10}^{ - 11}} \times {{(125 \times 1.67 \times {{10}^{ - 27}})}^2}}}{{2 \times {{10}^{ - 15}}}}$
$\Rightarrow V = \dfrac{{290655 \times {{10}^{ - 65}}}}{{{{10}^{ - 15}}}}$
$\Rightarrow V = 290655 \times {10^{ - 50}}$
Making an approximation,
$V \sim 3 \times {10^{ - 45}}$
Converting to eV we get,
$V \sim \dfrac{{3 \times {{10}^{ - 45}}}}{{1.6 \times {{10}^{ - 19}}}}$
$\therefore V \sim 1.875 \times {10^{ - 26}}$

So, the potential is of the order of -26.

Note: The distance is taken from the centers of the two bodies along the line of action of force. When the radius of the bodies is appreciably large, we take into account their radii as well while calculating the force. Else we take point masses and neglect their radii.The value of G is universal and does not depend on any factors like temperature, pressure and hence it is also called the universal gravitational constant.