Question

The 2nd, 3rd and 4th terms in the expansion of $(x + a)^n$ are 240, 720 and 1080, respectively.

The value of $(x – a)^n$ can be The sum of odd-numbered terms is

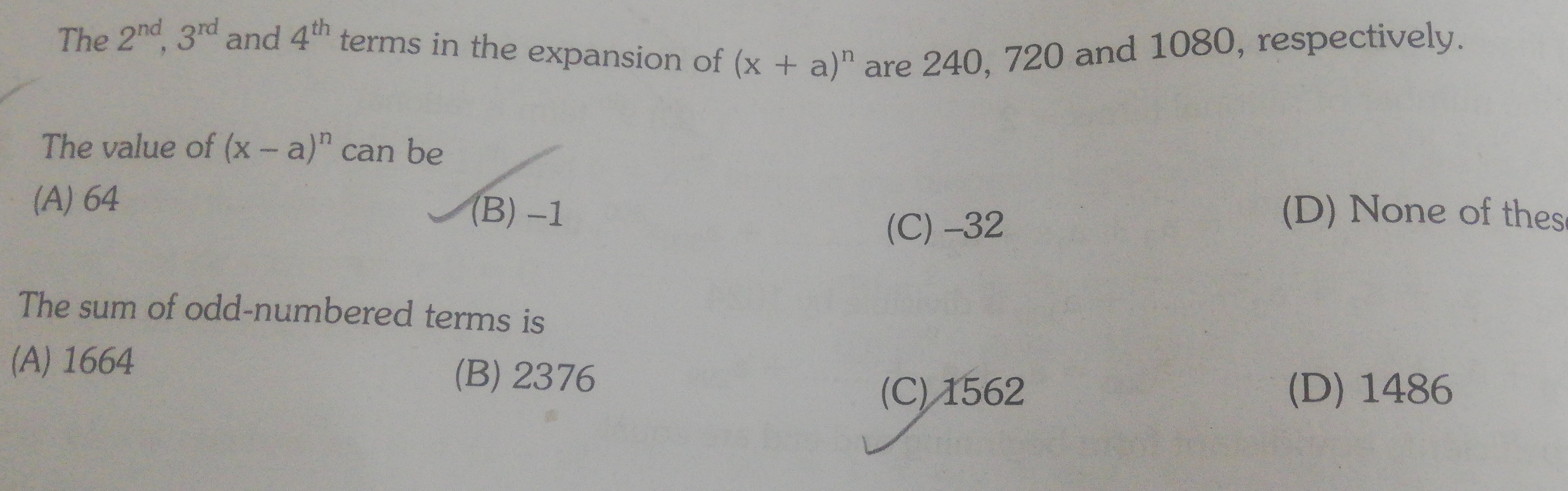
• A. 64
• B. -1
• C. -32
• D. None of these
• E. 1664
• F. 2376
• G. 1562
• H. 1486

Answer 1

Answer: (B), (G)

(B) -1 and (C) 1562

Answer 2

Given: $T_2 = 240$ $T_3 = 720$ $T_4 = 1080$

Using ratios of consecutive terms: $\frac{T_3}{T_2} = \frac{\binom{n}{2}x^{n-2}a^2}{\binom{n}{1}x^{n-1}a^1} = \frac{n-1}{2}\frac{a}{x} = \frac{720}{240} = 3$ (1) $\frac{T_4}{T_3} = \frac{\binom{n}{3}x^{n-3}a^3}{\binom{n}{2}x^{n-2}a^2} = \frac{n-2}{3}\frac{a}{x} = \frac{1080}{720} = \frac{3}{2}$ (2)

Dividing (1) by (2): $\frac{\frac{n-1}{2}\frac{a}{x}}{\frac{n-2}{3}\frac{a}{x}} = \frac{3}{3/2}$ $\frac{3(n-1)}{2(n-2)} = 2$ $3(n-1) = 4(n-2)$ $3n - 3 = 4n - 8$ $n = 5$

Substitute $n=5$ into (1): $\frac{5-1}{2}\frac{a}{x} = 3$ $2\frac{a}{x} = 3 \implies \frac{a}{x} = \frac{3}{2}$

Now, use $T_2 = \binom{5}{1}x^{5-1}a^1 = 5x^4a = 240$. Substitute $a = \frac{3}{2}x$: $5x^4(\frac{3}{2}x) = 240$ $\frac{15}{2}x^5 = 240$ $x^5 = 240 \times \frac{2}{15} = 16 \times 2 = 32$ $x = 2$

Then $a = \frac{3}{2}x = \frac{3}{2}(2) = 3$.

First part: $(x-a)^n = (2-3)^5 = (-1)^5 = -1$.

Second part: Sum of odd-numbered terms is $\frac{1}{2}[(x+a)^n + (x-a)^n]$. Sum = $\frac{1}{2}[(2+3)^5 + (2-3)^5]$ Sum = $\frac{1}{2}[5^5 + (-1)^5]$ Sum = $\frac{1}{2}[3125 - 1]$ Sum = $\frac{3124}{2} = 1562$.